34_Effekt Compton

Proprietatile cele mai complete corpusculare ale luminii sunt prezentate în efectul Compton. American fizician A. Compton (1892-1962), investigarea în 1923 împrăștierea materialelor cu raze X monocromatice cu atomi ușori (parafină, bor), a constatat că o parte din radiația împrăștiată în plus față de radiația inițială de λ lungime de undă se observă, de asemenea, radiația de lungimi de undă mai λ“. Experimentele au arătat că diferența de λ = λ „- λ este independent de lungimea de undă a radiației incidente și natura materialului de împrăștiere, și determinat numai de valoarea unghiul de împrăștiere:

λ = λ „- λ = λ 2 C păcatul 2 (θ / 2).

în cazul în care „lungimea λ a radiației împrăștiate, λ C - Compton lungime de undă. (In împrăștierea unui foton printr-un λ electron C = 2,426 nM).

efectul Compton se numește împrăștierea elastică a radiației electromagnetice de unde scurte (cu raze X și γ-radiație) asupra (cuplate sau slab) liber substanțele electroni, însoțite de o creștere a lungimii de undă. Acest efect nu se potrivește teoria ondulatorie conform căreia lungimea de undă a împrăștierii nu trebuie să varieze: sub acțiunea unui câmp optic periodic variază în funcție de frecvența câmpului de electroni și, prin urmare, emite undele împrăștiate de aceeași frecvență.

Explicația dată de Compton efect pe baza ideilor cuantice despre natura luminii. Dacă presupunem, la fel ca și teoria cuantică, că radiația are un caracter corpuscular, t. E. este un flux de fotoni, Compton e ffekt

- rezultatul ciocnirilor elastice sau y-x-ray fotoni cu substanta electroni liberi (pentru lumină legat slab atomi de electroni cu nucleele atomice, astfel încât acestea să poată fi considerate libere). In timpul acestei coliziuni de electroni transferă fotonice o parte din energia și impulsul său, în conformitate cu legile de conservare.

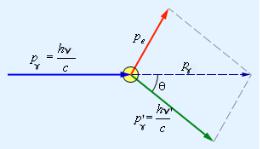
Fig. 1. Legea conservării impulsului în împrăștierea unui foton printr-un electron liber

Să considerăm o ciocnire elastică între două particule (Figura 1) - fotonul incident de

Expresia (11) nu este altul decât formula Compton obținută experimental. Substituind în ea valorile h. m 0. c dă lungimea de undă Compton

Prezența liniei undisplaced radiației împrăștiate (lungimea de undă a radiației inițială) poate fi explicată după cum urmează. Atunci când se analizează mecanismul de împrăștiere a presupus că un foton se ciocnește cu un electron liber. Cu toate acestea, în cazul în care electronul este puternic cuplat cu atomul cum este cazul electronilor interiori (în special în atomi grei), energia fotonilor și impuls este schimbat cu un atom ca întreg. Deoarece masa atomică în comparație cu masa unui electron este foarte mare, atunci atomul este transferat numai o parte nesemnificativă a energiei fotonice. Prin urmare, în acest caz, lungimea de undă a radiației împrăștiate nu este substanțial diferită de lungimea de undă a radiației incidente.

Din considerentele de mai sus, rezultă de asemenea că efectul Compton nu poate fi observată în domeniul vizibil, deoarece energia fotonului este comparabil cu lumina vizibilă cu energia de legătură a electronilor unui atom, în care electronul extern chiar imposibil să ia în considerare liber.

efect Compton se observă nu numai pe electroni, ci și pe alte particule încărcate, cum ar fi protoni, dar din cauza masei mari a protonului întoarcerea sa este privit doar în împrăștierea de fotoni cu energii foarte mari. Deoarece efectul Compton și efectul fotoelectric bazat pe reprezentări cuantice ale electronilor datorită interacțiunii cu fotoni. În primul caz, fotonul este disipată în al doilea

- absorbit. Scattering apare atunci cand un foton interactioneaza cu un electron liber, iar efectul fotoelectric - cu electroni legați. Se poate demonstra că

foton coliziune cu un electron liber nu se poate produce absorbtia de fotoni, deoarece acest lucru este în conflict cu legea conservării impulsului și energiei. Prin urmare, numai împrăștierea lor poate fi observată în interacțiunea fotonilor cu electroni liberi, t. Efectul E. Compton.

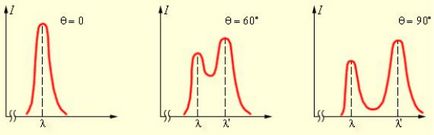
Fig. 2 prezintă rezultatele experimentale privind observarea imprastierii Compton în țintă din grafit cu un electron legat slab la nucleul atomic. Odată cu creșterea unghiului θ este prezentat mai clar semnal (dreapta în figură), asociată cu Compton.

Vârful din stânga corespunde o lungime de undă a fotonului incidente (în acest caz, așa-numita K a - linia de molibden). Acestea sunt fotonii care sunt împrăștiate fără schimbare

electronii cojile interioare. Primul grafic Compton este absent, θ = 0 °. Al doilea la θ = 60 ° arată un vârf asociat cu Compton, etc., cu creșterea unghiului de împrăștiere la θ = 90 ° vârf este deplasată de-a lungul axei orizontale proporțional crește cu lungimea de undă (conform formulei) care corespunde solubilității sale mai bine.

Evident, pentru a observa efectul necesită două condiții: 1. Lungimea de undă a radiației împrăștiate ar trebui să fie comparabile cu Compton