Ce este parte integrantă, și care este semnificația sa fizică

Aspectul a fost conceptul integral datorită nevoii de a găsi o funcție primitivă a derivatului său, și se determină valoarea de forme complexe din zona de lucru, distanța parcursă distanța, cu parametrii curbelor trasate de ecuații neliniare.

desigur

și fizica știm că munca este produsul de forță pe o distanță. Dacă toate mișcarea este la o viteză constantă sau distanța este depășită cu aplicarea aceeași forță, atunci totul este clar, pur și simplu multiplica. Care este integralei constanta? Aceasta este o funcție liniară a forma y = kx + c.

Dar puterea de operare poate varia și în unele relație ordonată. O situație similară apare cu calcularea distanței parcurse, în cazul în care viteza nu este constantă.

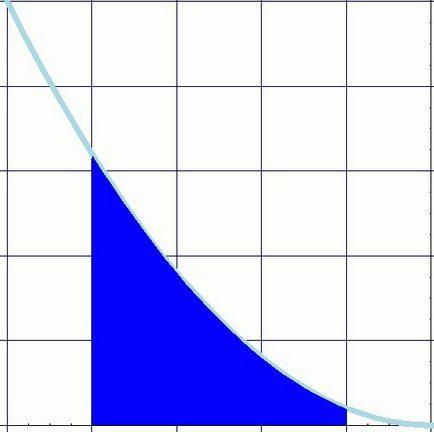
Deci, este de înțeles de ce există o parte integrantă. Definind-o ca o sumă de produse de valori ale funcției pe incrementul infinitezimal a argumentului descrie complet sensul principal al termenului ca aria figurii delimitat de linia de sus a funcției, și marginile - definirea limitelor.

Jean Gaston Darboux, matematician francez, în a doua jumătate a secolului al XIX-lea este foarte clar explicat că această integrantă. El a făcut-o atât de clar că un întreg nu va fi dificil de înțeles chiar și un elev liceu în această chestiune.

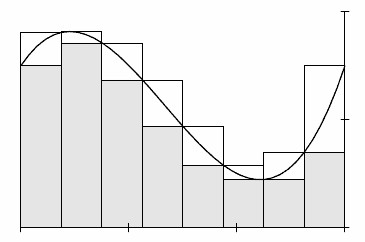
Să presupunem că există o funcție de orice formă complexă. Axa y, pe care sunt depuse valoarea argumentului, este împărțit în intervale mici, în mod ideal, acestea sunt infinit de mici, ci pentru că conceptul de infinit este destul de abstractă, este suficient să ne imaginăm bucăți doar mici, a cărei valoare este de obicei notată cu delta litera grecească (delta).

Funcția a fost „tăiate“ în blocuri mai mici.

Fiecare valoare a argumentului corespunde unui punct pe axa ordonatei la care depun valorile corespunzătoare ale funcției. Dar, așa cum limitele din zona selectată două, valorile și funcțiile vor fi, de asemenea, două sau mai multe și mai puțin.

Suma produselor de valori mari pentru incrementul δ Darboux numita cantitate mare, și este denumit S. Prin urmare, valori mai mici pentru o arie limitată, înmulțită cu δ, formează împreună o cantitate mică Darboux s. Site-ul în sine seamănă cu un trapez dreptunghiular, astfel încât în ​​funcție de curbura liniei din cauza unui increment infinitezimal poate fi neglijată. Cel mai simplu mod de a găsi zona unei forme geometrice - o piese îndoite de valori mai mari și mai mici ale funcției la δ-increment și se împarte la doi, care este definită ca media aritmetică.

Asta integralei Darboux:

s = σf (x) δ - o cantitate mică;

S = σf (x + δ) δ - cantitate mare.

Deci, ce este integrala? Zona delimitată de o funcție de linie și definirea limitelor va fi egal cu:

Adică, media aritmetică a sumelor majore și minore Darbu.s - valoare constantă, resetabil la diferențierea.

Bazat pe expresia geometrică a acestui concept, devine clar sensul fizic al integralei. forme pătrate, conturat în funcție de viteză, iar intervalul de timp limitat pe axa x va fi lungimea distanței parcurse.

L = ∫f (x) dx în intervalul de la t1 la t2,

f (x) - o funcție de viteză, adică formula prin care se modifică în timp;

L - lungimea căii;

t1 - ora de începere a traseului;

t2 - timpul de finalizare calea.

Exact același principiu este determinată de cantitatea de muncă, dar vor fi depuse pe abscisă distanța și ordonata - cantitatea de forța exercitată asupra fiecărui punct în parte.