Cea mai mare și cea mai mică valoare a funcției

Din punct de vedere practic, cel mai interesant este utilizarea de instrumente derivate, în scopul de a găsi cele mai mari și cele mai mici valori ale funcției. Care este motivul? Maximizarea profitului, minimizarea costurilor, determinarea utilizării optime a echipamentelor. Cu alte cuvinte, în multe domenii ale vieții, este necesar pentru a rezolva problema de optimizare a oricăror parametri. Și aceasta este problema de a găsi cele mai mari și cele mai mici valori ale funcției.

Trebuie remarcat faptul că valoarea maximă și minimă a funcției este solicitată în mod obișnuit într-un interval X. care este un întreg domeniu sau unei funcții sau o parte a domeniului de definire. Intervalul de auto X poate fi un interval infinit interval de segment deschis.

În acest articol vom vorbi despre găsirea valorilor minime ale unei funcții explicite a unei variabile y = f (x) și maxime.

Navigare în pagină.

Cea mai mare și cea mai mică valoare a funcției - definiție, ilustrare.

discuta pe scurt definițiile de bază.

Cea mai mare valoare a funcției y = f (x) în intervalul X se numește o valoare astfel încât pentru orice inegalitate.

Cea mai mică valoare a funcției y = f (x) în intervalul X se numește o valoare astfel încât pentru orice inegalitate.

Aceste definiții sunt intuitive: cea mai mare (mai mică), valoarea funcției - aceasta este cea mai mare valoare (cea mai mică) a primit la intervalul de la abscisă.

Punctele de staționare - sunt valorile argumentului, în care derivatul devine zero.

De ce punct fix atunci când valorile maxime și minime? Răspunsul la această întrebare este dat de ultima teorema a lui Fermat. Rezultă din aceasta teorema că în cazul în care o funcție diferențiabilă are un extremum (minim local sau maxim local) la un anumit punct, atunci acest punct este fix. Astfel, funcția ia adesea valoarea sa maximă (minimă) în intervalul X într-unul dintre punctele fixe ale acestui interval.

De asemenea, este de multe ori cea mai mare și cea mai mică valoare a funcției poate fi făcută la punctele în care există prima derivată a acestei funcții, iar funcția este definită.

Imediat răspunsul la una dintre cele mai frecvente întrebări pe tema: „Este întotdeauna posibil să se determine cea mai mare valoare (cea mai mică) a funcției“? Nu, nu întotdeauna. Uneori, intervalul de delimitare X coincide cu limitele domeniului de definire a funcției sau intervalul X este infinit. Și unele funcții la infinit și la granițele definițiilor de câmp pot fi luate ca infinit de mare și valorile infinit de mici. În aceste cazuri, nimic nu se poate spune despre cea mai mare și cea mai mică valoare a funcției.

Pentru claritate, vom da o ilustrare grafică. Uită-te la cifrele - și mult mai clare.

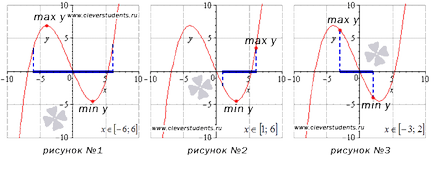
Prima funcție de imagine are cea mai mare (max y) și cea mai mică (min y) valorile la punctele de staționare, care sunt în interiorul intervalului [-6, 6].

Luați în considerare cazul prezentat în a doua imagine. Schimbati pe segmentul [1, 6]. În acest exemplu, cea mai mică valoare este atins la un punct fix, iar cel mai mare - punctul cu abscisa corespunzător marginea dreaptă a intervalului.

Figura №3 punctele de delimitare ale intervalului [-3, 2] sunt absciselor punctelor corespunzătoare celei mai mari și cea mai mică valoare a funcției.

La intervalul deschis

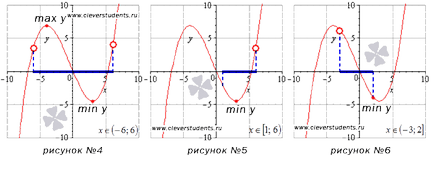
A patra Funcția de imagine are cea mai mare (max y) și cea mai mică (min y) valorile în punctele de staționare situate în intervalul deschis (-6, 6).

La interval [1, 6), cea mai mică valoare a funcției este realizată într-un punct de staționare, precum și despre cea mai mare valoare nu putem spune nimic. Dacă punctul x = 6 a fost o parte a intervalului, în timp ce atunci când această valoare a funcției ar lua cea mai mare valoare. Acest exemplu este prezentat în Figura №5.

Figura №6 cea mai mică valoare este atinsă la marginea din dreapta a intervalului (-3 ;. 2] cea mai mare valoare a oricăror concluzii pot fi trase.

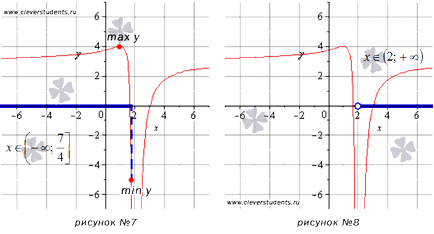
În exemplul prezentat în a șaptea figură, funcția are valoarea cea mai mare (max y) la un punct staționar cu abscisa x = 1. iar cea mai mică valoare (min y) se realizează la limita din dreapta a intervalului. La valori de minus infinit se apropie asimptotic de y = 3.

Funcția interval nu atinge cea mai mică sau cea mai mare valoare. Când lupta pentru x = 2 valori ale funcției dreapta tind să minus infinit (linia dreaptă x = 2 este o asimptotă verticală), iar abscisa tinde la infinit plus, valorile funcției se apropie asimptotic de y = 3. ilustrare grafică a acestui exemplu este prezentată în Figura №8.

Algoritmul pentru gasirea celor mai mari și cele mai mici valori ale unei funcții continue la intervalul [a, b].

Noi scrie algoritmul pentru a găsi cea mai mare și cea mai mică valoare a funcției pe intervalul.

1. Găsiți domeniul funcției, și verifică dacă întregul interval [a, b].
2. Găsiți toate punctele la care există primul derivat și care sunt cuprinse în intervalul [a, b] (de obicei, la astfel de puncte vstechayutsya funcționale cu un argument al semnului modulului și funcțiile de putere cu indicator fracționară rațional). Dacă aceste puncte nu au, atunci vom merge la pasul următor.
3. Se determină toate punctele staționare care se încadrează în intervalul [a, b]. Pentru a face acest lucru, găsim derivata funcției. echivalând-l la zero și pentru a rezolva ecuația rezultată selectați rădăcina corespunzătoare. În cazul în care nu există puncte de staționare, sau nici unul dintre ei trece aproape de tăiat, apoi du-te la pasul următor.
4. Noi calcula valorile funcției în punctele fixe selectate (dacă există) în punctele în care nu există nici un prim derivat (dacă există), și atunci când x = a și x = b.
5. Din valorile obținute ale funcției, selectați cel mai mare și cel mai mic - acestea sunt cele mai solicitate valori minime și maxime ale funcției, respectiv.

Să luăm în considerare algoritmul pentru rezolvarea exemplul de a găsi cele mai mari și cele mai mici valori ale intervalului.

Găsiți cel mai mare și cea mai mică valoare a funcției

• în intervalul [1, 4];
• în intervalul [-4, -1].

Să începem cu domeniul funcției. polinom pătratic în numitorul nu dispare:

Este ușor de verificat toate intervalele de condițiile problemei aparțin domeniului funcției.

Evident, derivatul există în întregul domeniu al funcției.

Noi găsim punctele de staționare. Derivata dispare la. Acest punct staționar se încadrează în intervalele (-3, 1] și (-3, 2).

Pentru o primă perioadă se calculează valoarea funcției x = -4 și o limită infinit minus:

De atunci, și pe cea mai mică valoare a funcției de concluzii pot fi trase. Se poate spune doar că valorile funcției sunt delimitate de mai jos printr-o valoare de -1 (valoarea funcției minus infinit se apropie asimptotic de o linie y dreaptă = -1).

Al doilea interval de interes, care nu conține nici un punct de staționare, și nici unul dintre ea nu este o limite stricte. În acest caz, nu putem găsi cea mai mare sau cea mai mică valoare a funcției. Calcularea limita la minus infinit și argumentul tinde la minus trei pe stânga, vom fi în măsură să determine intervalul valorilor numai:

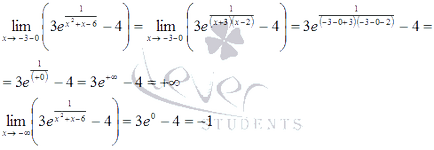
În consecință, valorile funcției sunt în intervalul de la x decalajul.

Pentru a treia perioadă (-3, 1] se calculează valoarea funcției în punctul de staționare și când x = 1 și limita unilaterală, argumentul tinde spre -3 dreapta :.

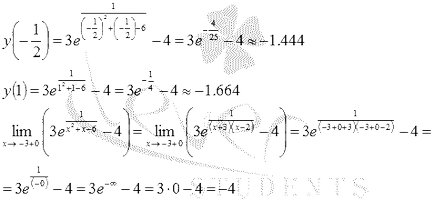
Prin urmare, cea mai mare valoare din acest interval funcția ia într-un punct de staționare, cea mai mică valoare a funcției, nu putem calcula, dar valoarea funcției este limitată de mai jos de -4.

Pentru intervalul (-3, 2) să utilizeze rezultatele din paragraful precedent și mai departe calcula limita sided tinde spre egalitate de puncte din stânga:

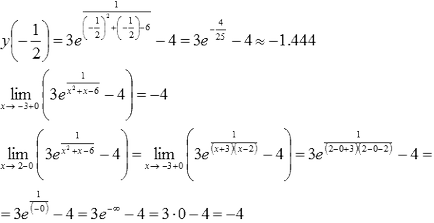
Prin urmare, cea mai mică valoare nu este posibil să se determine valorile funcțiilor sunt limitate de mai jos de -4.

Rezultatele celor două puncte anterioare sugerează că, în intervalul [1; 2) primește cea mai mare valoare a funcției x = 1. cea mai mică valoare nu poate fi găsit, valorile funcțiilor sunt limitate de mai jos de -4.

Funcția interval nu se ajunge la nici cea mai mare sau cea mai mică valoare.

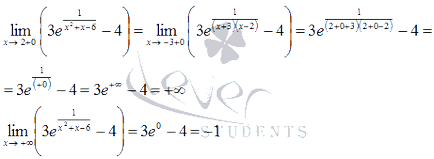
Aceasta este, în acest interval ia valori în intervalul.

Calcularea valorii funcției x = 4. se poate argumenta că, în funcție infinit plus se apropie asimptotic de o linie dreaptă y = -1.

Acum puteți compara rezultatele obținute la fiecare punct cu graficul funcției. Liniile punctate albastre indică asimptota.

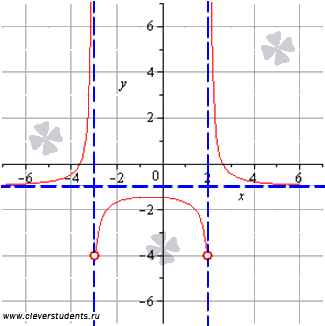
Pe aceasta puteți termina cu găsirea cele mai mari și cele mai mici valori ale funcției. Algoritmii înțeleg acest articol, permit obținerea unor rezultate cu acțiune minimă. Cu toate acestea, este util să se stabilească mai întâi intervalele de creștere și descreștere a funcției și numai apoi trage concluzii cu privire la cea mai mare și cea mai mică valoare a funcției la orice interval. Aceasta oferă o imagine mai clară și o justificare riguroasă a rezultatelor.