Cum de a determina paralelismul a două linii

Liniile paralele sunt numite linii drepte care se află într-un singur plan și niciodată nu se intersectează (pentru infinit). [1] În aceeași pantă drepte paralele. [2] Panta egală cu panta liniei la abscisă, și anume coordonate relative schimbare «y» pentru a schimba coordonatele „x“. [3] De multe ori, liniile paralele sunt indicate de «ll». De exemplu, înregistrarea ABllCD înseamnă că linia AB este paralela cu CD.

pași Editare

Metoda 1 de la 3:
O comparație a pârtiilor din cele două drepturi drepte

Se înregistrează formula de calcul a pantei. Formula: k = (y2 - y1) / (x2 - x1), unde «x» și «y» - coordonatele două puncte (orice) situată pe o linie dreaptă. Coordonatele primului punct, care este mai aproape de originea, ca etichetă (y1 x1.); coordonează al doilea punct, care este mai departe de origine, ca etichetă (x2. y2). [4]

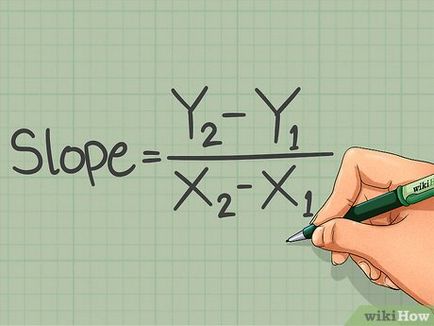
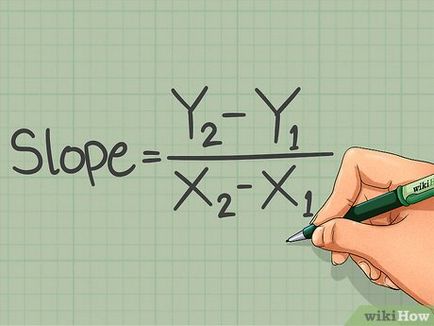
• Formula de mai sus se poate afirma astfel: raportul dintre distanța verticală (între puncte) la distanța orizontală (între două puncte).
• În cazul în care crește linia (îndreptată în sus), coeficientul său unghiular este pozitiv.
• Dacă linia scade (îndreptată în jos), colțul de coeficient negativ.

Se determină coordonatele a două puncte care se află pe fiecare linie. Coordonatele punctelor înregistrate în forma (x, y), unde „x“ - coordonata de-a lungul axei X (abscisă), «y» - coordonata pe axa „y“ (axa y). Pentru a calcula panta, marca două puncte pe fiecare linie. [5]

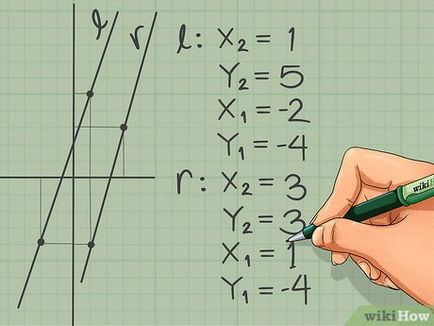
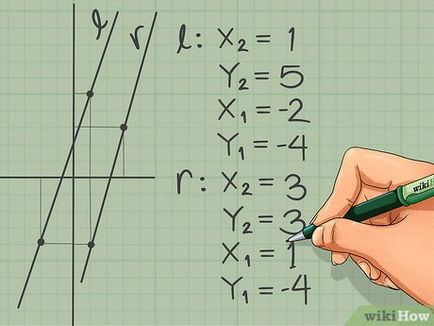
• Ușor de punct de notat, în cazul în care liniile trasate pe planul de coordonate.
• Pentru a determina coordonatele unui punct, trage din ea perpendicularele (imaginar) pentru fiecare axă. Punctul de intersecție al liniei punctate cu axa X - este coordonata „x“, iar punctul de intersecție cu axa Y - coordonate „y“.
• De exemplu: pe o linie l conține punctele cu coordonate (1, 5) și (-2, 4) și pe linia r - coordonatele punctului (3, 3) și (1, 4).

Puneți coordonatele punctelor în formulă. Apoi scade coordonatele corespunzătoare și de a găsi raportul dintre rezultatele obținute. Prin substituirea coordonatele în formula nu le se amestecă în ordine.

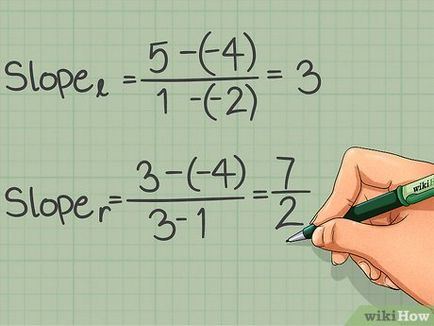
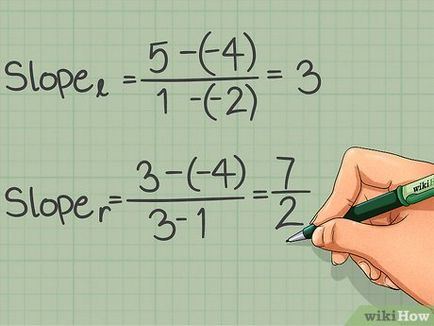
• Calculul pantei liniei l: k = (5 - (-4)) / (1 - (-2))
• Scadere: k = 9/3
• Divizia: k = 3
• Calculând panta unei linii drepte r: k = (3 - (-4)) / (3 - 1) = 7/2

Comparați coeficienții unghiulare. Amintiți-vă că liniile paralele coeficienți unghiulare sunt egale. Cifra poate părea dreaptă paralelă, dar în cazul în care coeficientul unghiular nu este egal, astfel de linii nu sunt paralele între ele. [6]

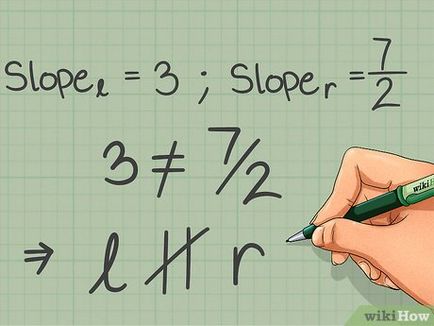
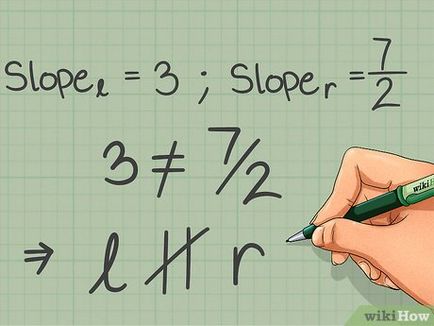
• În acest exemplu, 3 nu este egal cu 7/2, astfel încât liniile de date nu sunt paralele.

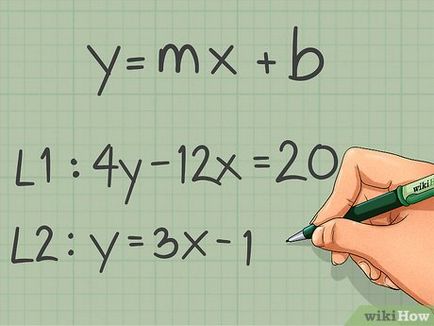
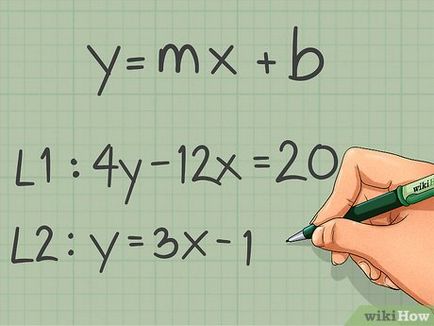
ecuație liniară înregistrare. Ecuația liniară este y = kx + b, unde k - panta, b - coordonate punctul „y“ intersecția liniei Y cu axa „x“ și „y“ - variabile coordonate ale punctelor care se află pe o linie dreaptă definite. În conformitate cu această formulă se poate calcula cu ușurință coeficientul unghiular k. [7]

• De exemplu. Prezentați ecuația 4y - 12x = 20 și y = 3x -1 sub forma unei ecuații liniare. Ecuația 4y - 12x = 20 necesitatea de a fi reprezentat în forma cerută, dar ecuația y = 3x -1 a fost deja înregistrată ca o ecuație liniară.

Rescriem ecuația ca o ecuație liniară. Uneori dat ecuație, care nu este reprezentat sub forma unei ecuații liniare. Pentru a rescrie această ecuație, trebuie să efectuați o serie de operații matematice simple.

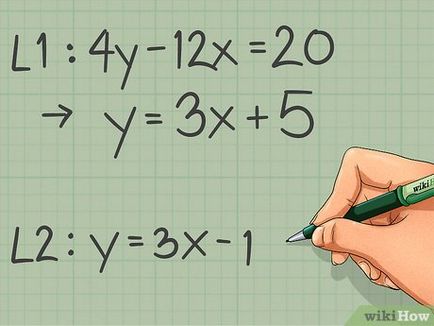
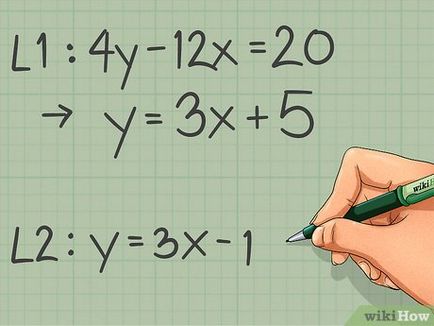
• De exemplu: rescrie ecuația 4y - 12x = 20 sub forma unei ecuații liniare.
• Pentru ambele părți ale ecuației, se adaugă 12x: 4y - 12x + 12x = 20 + 12x
• Ambele părți ale ecuației sunt împărțite în 4 pentru a izola „in»: 4y / 4 = 12x / 4 +20/4
• Sub formă de ecuație liniară: y = 3x + 5.

Comparați coeficienții unghiulare. Amintiți-vă că liniile paralele coeficienți unghiulare sunt egale. Folosind ecuația y = kx + b, unde k - panta poate găsi și compara pantele celor două linii.

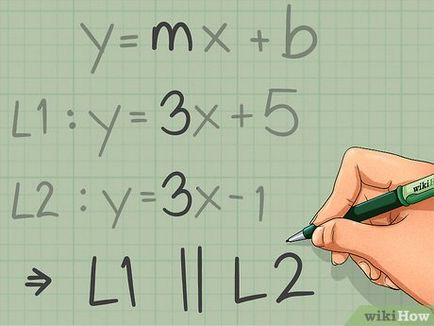
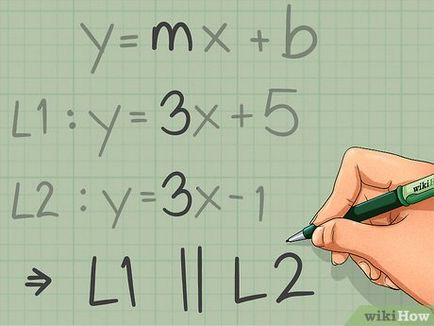
• În exemplul nostru, prima linie dreaptă este descrisă de ecuația y = 3x + 5, astfel încât panta este 3. A doua linie dreaptă este descrisă de ecuația y = 3x - 1, deci coeficientul unghiular este de asemenea egal cu 3. Deoarece coeficienții unghiulare sunt egale, liniile de date sunt paralele.
• Rețineți că, în cazul în care liniile cu pantă egală cu coeficientul b (coordonate „y“, punctul de intersecție al liniei drepte cu axa Y) este de asemenea identic, aceste linii drepte coincid și nu sunt paralele. [8]

Metoda 3 din 3:
Găsirea ecuația unei linii paralele direct la Edit

Notați ecuația. Următoarea ecuație permite să găsească ecuația liniei paralele (a doua), în cazul dat ecuația primei linii drepte și punctul care se află pe paralela dorită (a doua), linia de coordonate: y - y1 = k (x - x1), unde k - panta, x1 și y1 - coordonatele punctului de pe linia dorită, „x“ și „y“ - variabilele care determină coordonatele punctelor care se află pe prima linie dreaptă. [9]

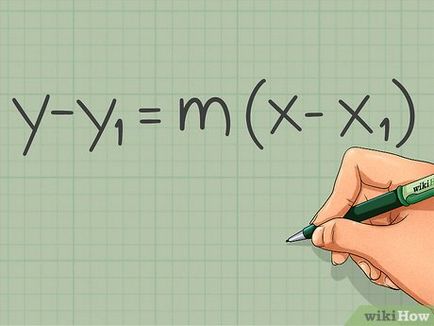
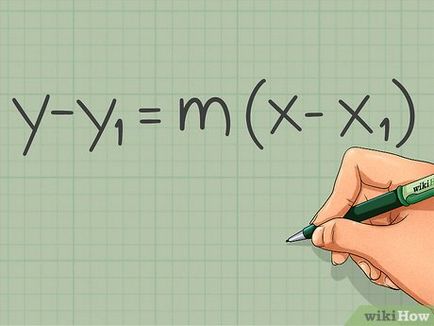
• De exemplu: găsiți ecuația liniei care este paralelă cu linia y = -4x + 3 și care trece prin punctul (1, -2).

Se determină panta (prima) linie. Pentru a găsi ecuația liniei paralele (a doua), trebuie să stabilească mai întâi panta. Asigurați-vă că ecuația este dată sub forma unei ecuații liniare, iar apoi găsiți valoarea coeficientului unghiular (k).

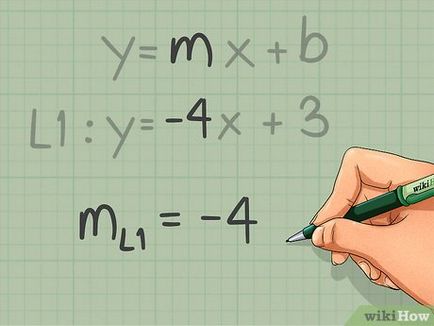
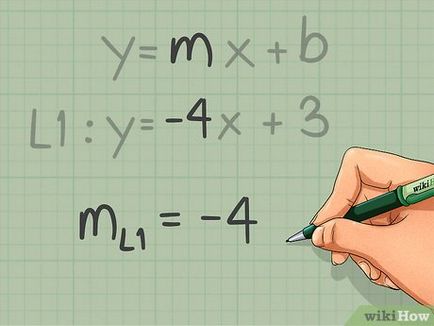
• A doua linie dreaptă trebuie să fie paralelă cu o anumită linie, care este descris de ecuația y = -4x + 3. În această ecuație, k = -4, astfel încât a doua linie este aceeași pantă.

Așa cum este reprezentat de ecuația înlocui un punct care se află pe o a doua linie de coordonate. Această metodă se aplică numai în cazul în care coordonatele date ale unui punct care se află pe a doua linie, ecuația de care trebuie să fie găsit. A nu se confunda coordonatele acestui punct cu coordonatele unui punct care se află pe acea (prima) linie. Rețineți că, în cazul în care liniile cu pantă egală cu coeficientul b (coordonate „y“, punctul de intersecție al liniei drepte cu axa Y) este de asemenea identic, aceste linii drepte coincid și nu sunt paralele.

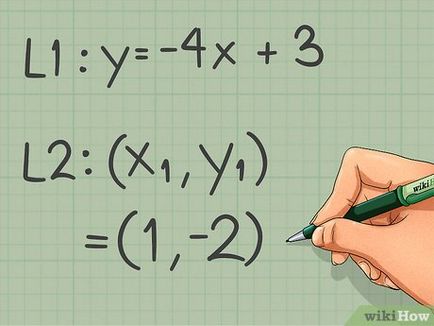
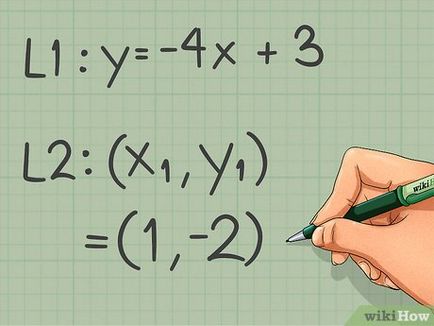
• În exemplul nostru, situată pe al doilea punct linie dreaptă are coordonatele (1, -2).

Notați ecuația a doua linie. În acest scop, valorile cunoscute pentru a substitui în ecuația y - y1 = k (x - x1). pantă substitut găsit și coordonatele unui punct care se află pe a doua linie.

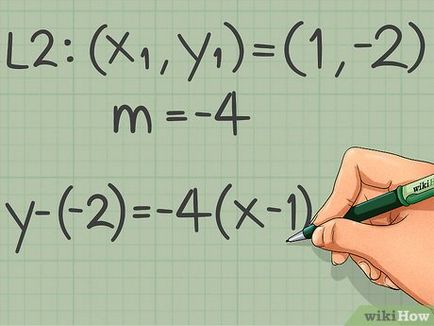
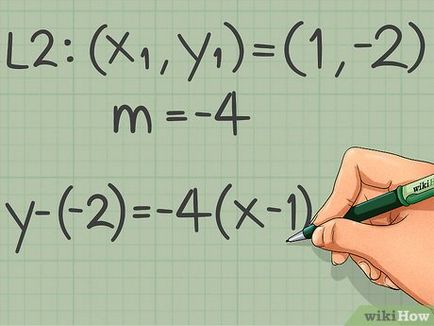
• In exemplul nostru, k = -4, iar coordonatele punctului (1, -2) y - (-2) = -4 (x - 1)

Simplificati ecuația. Simplificati ecuația și scrie sub forma unei ecuații liniare. Dacă desenați oa doua linie pe un plan de coordonate, va fi paralelă cu dată (prima) linie.

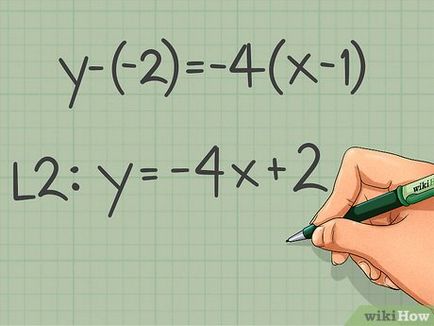
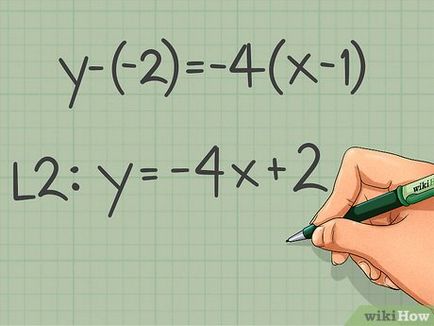
• De exemplu: - (-2) = -4 (x - 1)
• Două "minus" da "plus": y 2 = -4 + (x-1)
• Extindeți suporturile: y + 2 + 4 = -4x.
• Din ambele părți ale ecuației scade -2: Y + 2 - 2 = -4x + 4 - 2
• O ecuație simplificată: y = -4x + 2