Cum de a găsi aria unei formule pătrat, o decizie desemnează cum să numere

Piața - figura geometrică care reprezintă un patrulater drept cu unghiuri egale și laturi. Astfel, un pătrat poate fi numit un dreptunghi ale cărui laturi sunt egale cu diamant sau adiacente, în care toate unghiurile sunt unghiuri drepte (egale cu 90 de grade).

Luați în considerare o varietate de sarcini pentru a găsi zona de pătrat.

Dacă se cunoaște o latură pătrat (a), suprafața (S) de suprafață este egală cu pătratul laturile sale:

Dacă specificați un perimetru pătrat (P), zona este egală cu saisprezecea a perimetrului pătrat:

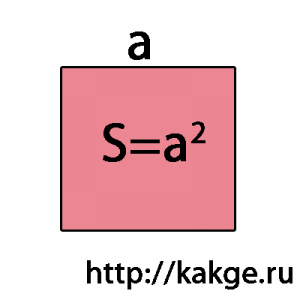
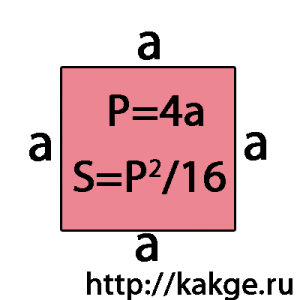
Dacă pătrat înscrisă în cerc și raza sa cunoscută (r), zona este egală cu raza la pătrat înmulțit cu 4:

O rază a unui cerc înscris într-un pătrat, la rândul său, este egală cu jumătate din lungimea laturii unui pătrat:

Dacă cunoscută raza cercului rotund pătrat (R), o zonă de pătrat este egală cu pătratul razei cercului circumscris înmulțit cu 2:

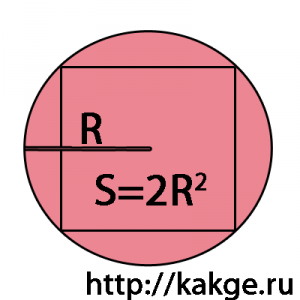
O rază de cerc circumscris în jurul unui pătrat, la rândul său, este egală cu jumătate din diametrul unui pătrat.

În cazul dat un pătrat diagonală (d), zona de pătrat este a doua putere diagonală împărțit la 2 (aceasta rezultă din teorema lui Pitagora):

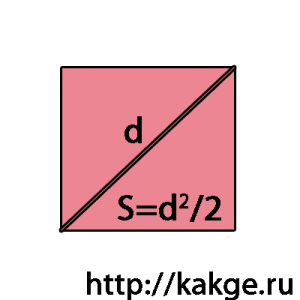
a² + a² = d² - teorema lui Pitagora (într-un triunghi dreptunghic este egală cu pătratul lungimii ipotenuzei unei sume de pătrate de lungimile picioarelor).