Cum se calculeaza conductele de greutate (Masu) și alte metale din

În lipsa posibilităților de cântărire directă, masa de metal poate fi, de asemenea, instalate în alte moduri. Rezultatele cele mai exacte va calcula, dar nu trebuie neglijat, și alte caracteristici.

Deci, pentru a nu încărca cititori formule redundante care vor fi în continuare, dar denote dreapta jos cu formula de calcul a celor mai populare produse din oțel și țevi laminate - țeavă de rulare. Nu veți găsi un calculator online pentru a calcula greutatea unei formule, amintiți-vă că o dată nu trebuie să utilizeze calculatorul speciale. De exemplu, atunci când îndepărtarea structurilor metalice sau horn. Eu nu au întotdeauna la îndemână un calculator, Internet sau un catalog, și toate construcție sudată din laminate aici si ajuta formula noastra!

Formula pentru a calcula greutatea țevii

• M - greutatea unui metru de țeavă în kg;
• D - diametrul exterior al țevii calculat, mm;
• s - grosimea peretelui țevii, mm;
• 0.02466 coeficient devin egale la o densitate de 7,850 g / cm3.

Această formulă este foarte precisă. Puteți calcula greutatea conductei și verificați greutatea estimată a teoretice în orice interval și valoarea formulei este mai precisă! De asemenea, puteți calcula

Ne așteptăm ca foi de metal greutate

• M - masa tablei de oțel, în kg;
• S - calculat suprafața foliară, în metri pătrați;
• 7,85 - greutate foaie de 1 mm grosime și o suprafață de 1 metru pătrat, în kilograme

Deci, este posibil să se calculeze greutatea tablei de orice dimensiune, de la care se poate calcula zona. Precizia acestei formule de calcul este mai mare decât masa teoretică în manuale, ca Gauge în calcularea masei valorilor metalice ale runde de program. Dar cum de a găsi zona a foii (de orice formă - pătrată, dreptunghiulară, paralelipipedică, trapez, romburi, etc.) - toată lumea ar trebui să știe o persoană care a absolvit liceul.

Cum se calculează greutatea armăturii și tija

Pentru cerc, tijă, formula montare buna pentru calculul masei este după cum urmează:

• M - gama de masă de 1 metru / supapă / tijă kg;
• D - diametrul cercului;
• 0.02466 coeficient devin egale la o densitate de 7.850 g / cm3
  

Pentru a calcula greutatea armăturii ondulat (A2, A3), poate și ar trebui să utilizeze aceeași formulă! Discrepanțele cu masa teoretică nu va fi, în ciuda diferitelor modele de secțiuni transversale.

O grămadă de fier vechi, desigur, imposibil de calculat fără cântărire formulele

abordări comune sau teorie ușor plictisitoare

Pentru a determina greutatea oricărui obiect este suficientă pentru a se multiplica volumul său de greutatea specifică. În cazul în care greutatea specifică este mai mult sau mai puțin clare, cu atât mai dificil de a determina volumul (dacă nu ia în considerare o astfel de formă de simplu ca un cub). Principiul cel mai general de calcul al volumului este considerat a fi principiul Gulden, în cazul în care aria secțiunii transversale a unui obiect înmulțită cu înălțimea. Cu o înălțime a structurilor metalice și a problemelor de obicei, nu apar, este ușor (sau aproape perfect) pentru a măsura în mod direct, în special în cazul în care înălțimea secțiunii transversală este constantă. Deci, putem trece împotriva oricărei secțiuni de țevi de oțel și profile, I-grinzi, canale, unghiuri, etc. Metoda de determinare a masei obiectelor metalice de forme complexe și non-ajustare va lua în considerare mai târziu.

Volumul piramidei

Piramidal final măciulie de garduri din oțel forjat, șicanele și alte părți ale structurilor metalice sunt comune. Volumul piramidei este ușor de calculat cu formula:

Deoarece baza de tehnologie a piramidei poate fi un pătrat, dreptunghi sau triunghi, atunci problema este rezolvată destul de simplu.

Volumul unei piramide trunchiate

formă de piramidă trunchiată sunt protejarea capace, încuietori de siguranță și uși. În astfel de situații, utilizați dependența:

• h - înălțimea de trunchi de piramidă;
• F - suprafața bazei sale mai mari;
• f - suprafața de bază mai mică.

În cazul în care o parte a unei structuri piramidale, a donat pentru fier vechi, unele deformate, se adaugă sau eliminate din fiecare dintre părți suma lipsă.

Volumul penei și obeliscul

Wedge în arta adesea este pentahedron, baza căreia se află un dreptunghi, iar fețele laterale sunt triunghiuri isoscele sau trapeze. Formula de calcul a volumului penei este după cum urmează:

• și - o parte piciorul de bază a penei;
• a1 - lățimea vârfului penei;
• b - grosimea penei;
• h - înălțimea penei.

Obelisc - un hexagon, baza care sunt dreptunghiuri, care sunt dispuse în planuri paralele. În care fețele opuse sunt înclinate simetric în partea de jos a obeliscului. Volumul corpului geometric:

• a și b - lungime și lățime mai mare obelisc de bază;
• și a1 și b1 - baza mai mică a obeliscului;
• h - înălțimea obeliscului.

Volum tijă și tub

Pentru calculul secțiunilor geometrice, care se bazează pe cerc, nu se poate face fără un parametru π - 3,14 (precizie mai mare pentru deșeuri metalice nu este necesară). Apoi cilindrul avem:

• R - raza tijei;
• H - lungimea / înălțimea barei.

Pentru o țeavă (cilindru tubular) Volumul se calculează cu formula:

r - raza tubului interior.

Volumul conului și trunchi de con

Forma geometrică a unui con de con și trunchi este utilizat pe scară largă în construcția de părți de mecanisme și mașini. Volumul conului este egal cu:

• R - raza bazei conului;
• H - înălțimea conului.

Pentru a calcula volumul trunchiului de con este utilizat o relație mai complexă:

R - raza bazei mici a conului.

Volumul elementelor sferice ale structurilor metalice

În plus față de propria sferă, în practică, este necesar să se ia în considerare, de asemenea, volumul unui segment sferic și de sector. Sunt utilizate următoarele relații:

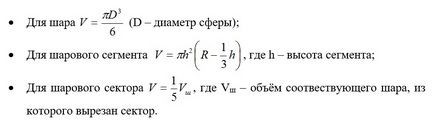
Volumele laminate

Cel mai adesea necesară pentru a determina greutatea Tauri, I-grinzi, canale, unghiuri. Următoarele relații se utilizează pentru:

unde b și b1 - respectiv lățimea raft și perete de brand; h și h1 - grosimea flanșei de bază și de brand; H - înălțimea deșeului fragmentului teu;

Pentru I-beam

unde H - înălțimea / lungimea elementului în formă de I; și - grosimea peretelui de fază I; c și c1 - I-beam Grosimea flanșei la bază și pe fața de capăt, respectiv;

în colțul

,unde H - lungimea de colț; l1 - grosimea de colț; h1 și h2, respectiv, - lățimea fiecăreia dintre rafturi.

Cum se instalează o mulțime de design foarte complex forma

Soluția la această problemă poate fi rezolvată în două moduri. Conform primei valoare set de așa-numitul factor de umplere (metoda este aplicată ansamblurilor de marcare, dezasamblarea sunt fie dificil sau nu este posibil deloc). De exemplu, pentru glisiera mașini de manivelă Factorul de umplere trebuie să fie egală cu 0,3 ... 0,35. Apoi găsește ansamblul de greutate G, în ipoteza că acesta este un solid, apoi înmulțiți rezultatul cu raportul taxei.

Despre aceeași acuratețe oferă o formulă empirică Nistratova:

, unde P - forța nominală de presă în tone.

Puteți seta numărul inițial de mici construcții-o singură bucată din volumul de apă deplasat de acestea. La aceasta se toarnă într-un recipient tarată până la marginile apei. Montat într-un alt recipient cu un volum mult mai mare, și apoi plasat în primul rezervor dat de proiectare. Volumul deplasat de apă cântărit. Această sumă va fi egal cu volumul structurii.