Determinate de mărimea și direcția vitezei în punctul de coordonate metoda de referință al mișcării

Acasă | Despre noi | feedback-ul
Care sunt modalitățile de specificare a mișcării unui punct utilizat în cinematica și ceea ce sunt? Cum de a determina traiectoria modului atunci când punctul de locuri de muncă coordonatei?
Punctul de mișcare în spațiu este determinată de trei moduri de bază: un vector, coordonate și naturale.
Vector: vom alege un centru fix O și trage din punctul central M, care studiul de mișcare, vectorul raza r. Când mișcarea punctului M modificările vectoriale rază în mărime și direcție. Fiecare punct de timp corespunde unei anumite valori t r. Prin urmare, vectorul razei determină în mod unic poziția punctului M, astfel încât să se determine punctul de circulație, este necesar să se stabilească vectorul rază în formă de o singură dată continuu funcția r: r = r (t).
Ordonată: Dacă punctele de coordonate sunt definite ca o singură valoare în funcție de timp: x = x (t), y = y (t), z = z (t), poziția punctului M în spațiul este cunoscută în fiecare moment. Aceste ecuații definesc legea de mișcare a unui punct și sunt numite ecuațiile mișcării sale.
Natural: Această metodă este folosită în sarcina de mișcare atunci când traiectoria unui punct în raport cu sistemul de referință selectat este cunoscut. Atunci când se deplasează de coordonate curbilinii a punctului M s va varia în timp, adică: s = s (t). Cunoscând această ecuație, putem determina poziția fiecărui punct în timp. Se numește ecuația de mișcare și legea de mișcare de-a lungul unei căi predeterminate.
Definim poziția unui punct în spațiul de coordonate al unui anumit: x = x (t), y = y (t), z = z (t) (*). Pentru a determina poziția unui punct la momentul inițial (t = 0) este necesară în ecuația (*) pentru a substitui t = 0. Acum, pentru a determina traiectoria punctelor: s = s (t) folosiți lungimea arcului cu formula curbei: sau, având în vedere faptul că diferențierea se face în timp, ea poate fi rescrisă ca. Semnul „+“ este luată în cazul în care punctul se deplasează în direcția pozitivă cu curbilinie de referință de coordonate s.
Ce relație există între vectorul raza unui punct în mișcare și vectorul de viteză al acestui punct? Ca viteza de mișcare vector curbilinie dirijată a unui punct în raport cu traiectoria?
Descompunem vectorul raza unei coordonate carteziene vectori unitate de sistem :. Acum vom diferenția ecuația în funcție de timp. Rezultatul este o rată de descompunere a vectorilor unitare. . expansiune poate fi reprezentat după cum urmează :. în cazul în care. . - proiecția vectorului de viteză pe axele de coordonate. Astfel, proiecțiile privind carteziene viteză fixă axe de coordonate sunt egale cu un prim derivat în raport cu timpul de coordonatele corespunzătoare ale punctului în mișcare.
In vector: Pentru a calcula cu precizie viteza punctului la un moment dat, trebuie să meargă în formula pentru perioada limită de timp tinde la zero, adică :. Această limită este prima derivata a vectorului vectorului de raza la un moment de timp. După cum se poate observa din aceste formule, vectorul viteză este direcționat de-a lungul tangenta la traiectoria mișcării sale în direcția.
Când coordonate: Vom găsi rata unitară, știind proiecția sa :. Pentru a determina direcția vitezei de utilizare a vectorului cosinusului direcție:
. . . Ca urmare, încă prizhzhem la concluzia că vectorul viteză este direcționat de-a lungul tangenta la traiectoria.
Cu :. naturale știm că. Vectorul este un vector tangent unitate la calea (vectorul unitate) îndreptat spre ascendentă coordonate curbilinii s. Notând vectorul tangent inițial unitate de scriere ca formula :. multiplica partea stângă și dreaptă a ecuației pe vectorul unității. . Rescriem expresia după cum urmează :. Astfel, se observă că vectorul viteză direcționată tangențial la punctul de traiectorie.
Determinate de mărimea și direcția vitezei în punctul metodei de coordonate a sarcinilor de mișcare?
. . Astfel, proiecțiile privind carteziene viteză fixă axe de coordonate sunt egale cu un prim derivat de-a lungul timpului a coordonatelor corespunzătoare punctului în mișcare. Din ecuațiile rezultă că punctul de proiecție a vitezei pe axe de coordonate sunt proiecțiile vitezei acestui punct pe aceeași axă. Cunoscând proiecția vectorului de viteză a punctului, găsi modulul său :.
Pentru a determina direcția vitezei de utilizare a vectorului cosinusului direcție:
Ce relație există între vectorul raza unui punct în mișcare și vectorul accelerație al unui punct? Ca regia, vectorul accelerație a mișcării curbată a unui punct în raport cu traiectoria sa, acesta se află într-un plan?
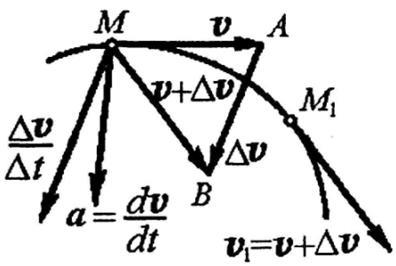
Acum Stabilim vectorul de poziție în raport cu calea. Rețineți că MAV plan triunghiul format vectori. și. când se rotește în jurul vectorului. și anume în jurul valorii de tangenta la traiectoria de la punctul F, și este nevoie de o anumită limită în poziția limită. Această poziție limită se numește planul MAP osculating plan la calea M punct. vector medie accelerație este îndreptată în același mod ca și. și anume în concavitatea curbei, și tot timpul să fie în planul MAB triunghi. Limita vector într-un vector. care se află în poziția de limitare a triunghiului MAB adică în planul osculating al traiectoriei punctului M. Astfel, vectorul punctului de accelerație complet este situată în planul osculating traiectoriei M este îndreptată spre concavitatea traiectoriei.