Funcții date parametrically
Legătura dintre argumentul și funcția poate fi scrisă în funcție de variabila suplimentare, numite parametri, adică, un sistem în care dependența prescrisă de argumentul parametrului și dependența funcției de aceiași parametri:
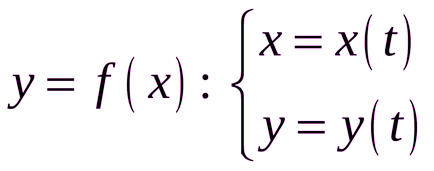

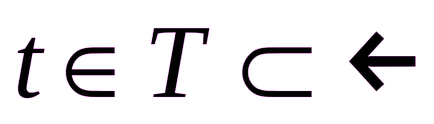
În acest caz, nazyvaetsyafunktsiey funcție definită parametric.
Graficul funcției y = f (x) este multimea tuturor punctelor ale căror absciselor aparțin domeniului funcției, iar valorile ordonatelor sunt egale cu funcția corespunzătoare.
Cu alte cuvinte, graficul funcției y = f (x) - este multimea tuturor punctelor din planul, coordonatele x, y satisfac relația y = f (x).
Comportamentul element de bază al funcției
Funcția y = f (x) este chiar dacă îndeplinește următoarele două condiții:
1. Domeniul de determinare a acestei funcții trebuie să fie simetrice în jurul punctului O. Aceasta este, în cazul în care un punct aparține unui domeniu al funcției, punctul de -a corespunzător trebuie să aparțină domeniului unei funcții date.
2. Valoarea funcției în punctul x aparținând domeniului funcției trebuie să fie egală cu valoarea funcției în punctul -x. Aceasta înseamnă că pentru orice punct x în domeniul funcției trebuie să satisfacă următoarea ecuație f (x) = f (-x).
Dacă desenați un grafic al unei functii, acesta va fi simetric în raport cu axa y.
De exemplu, funcția trigonometrică y = cos (x) este chiar
Funcția y = f (x) este numit ciudat dacă îndeplinește următoarele două condiții:
1. Domeniul de determinare a acestei funcții trebuie să fie simetrice în jurul punctului O. Aceasta este, în cazul în care un punct aparține unui domeniu al funcției, punctul de -a corespunzător trebuie să aparțină domeniului unei funcții date.
2. Pentru fiecare punct x în domeniul funcției trebuie să satisfacă următoarea ecuație f (x) = -f (x).
Graficul unei funcții impare este simetrică în raport cu punctul O - originea.
De exemplu, funcția trigonometrică y = sin (x), y = tg (x), y = ctg (x) este impar.
Funcția y = f (x) este periodică dacă există un anumit număr T! = 0 (numită perioada funcției y = f (x)), astfel încât pentru orice valoare a lui x în domeniul definiției funcției, numărul x + T si x T de asemenea, aparțin domeniului funcției și următoarea egalitate f (x) = f (x + T) = f (xT).
Trebuie să se înțeleagă că în cazul în care T - perioada funcției, numărul de k * T, unde k este orice alta decât zero număr întreg, va fi, de asemenea, o perioadă a funcției. Pe baza celor de mai sus, constatăm că orice funcție periodică are un număr infinit de perioade. Cel mai adesea, conversația este despre cele mai mici elemente de epocă.
păcat funcția trigonometrică (x) și cos (x) sunt periodice cu o perioadă egală cu cea mai mică de 2 * tt.
Funcții trigonometrice tg (x) și ctg (x) sunt periodice cu o perioadă egală cu cea mai mică tt.
Funcția y = f (x), definit pe X. set numit delimitate de mai sus, în cazul în care o pluralitate de valori limitate varf. Cu alte cuvinte, funcția f este mărginită de mai sus în cazul în care există o M constantă că are loc inegalitatea pentru fiecare.
Funcția y = f (x), definite pe setul X se numește mărginită de mai jos dacă setul valorilor sale este limitată de mai jos, adică, în cazul în care există o M constantă care kazhdogovypolnyaetsya inegalitatea. De exemplu, acestea sunt funcțiile exponențială, funktsiiy = x2n, y = x.
Funcția f (x), definite pe setul X, numit limitat. în cazul în care setul de valori sale este limitată atât de sus și de jos. Exemple de funcții care sunt delimitate pe linia reală, este o funcție y = sin x, y = cos x, y = ARccOS x, y = arcsin x, y = arctg x, y = arcctg x.
a) în cazul în care pentru toate x de la un anumit set de inegalități x f (x)> M și g (x) b) în cazul în care pentru toate x de la un anumit set de inegalități x f (x) M și g (x) M. unde M - un număr, apoi setați X la ecuația f (x) = g (x) este echivalent cu sistemul În cazul în care funcția este în creștere sau în scădere pe unele interval de timp, atunci se numește monotonă pe acest interval. Rețineți că, dacă f - o funcție monotonă a intervalului D (f (x)), atunci ecuația f (x) = const poate avea mai mult de o rădăcină în acest interval. Într-adevăr, dacă x1 Enumerăm proprietățile funcțiilor monotone (se presupune că toate funcțiile definite pe un anumit interval D). Suma de mai multe funcții în creștere este o funcție crescătoare. Lucrare funcția de creștere nenegativ este o funcție crescătoare. Dacă funcția f este mărită, atunci funcțiile cf (c> 0) și f + c, de asemenea, crește, iar funcția cf (c <0) убывает. Здесь c – некоторая константа. În cazul în care crește f și își păstrează semnul său, funcția 1 / f scade. În cazul în care funcția f este în creștere și este non-negativ, în cazul în care, de asemenea, crește. Dacă crește f și n - un număr impar, atunci fn este în continuă creștere. Compoziția g (f (x)) creșterea funcțiilor f și g, de asemenea, crește. Funcții elementare de bază