Funcții definite parametric

Luați în considerare linia de referință în planul în care variabilele x, y sunt funcții ale treilea t variabilă (parametru cunoscut):

Pentru fiecare valoare a lui t într-un anumit interval corespund anumite valori ale lui x și y, o. De aceea, un anumit plan punct M (x, y). Când t variază peste toate valorile intervalului stabilit, atunci punctul M (x, y) descrie anumite linii L. Ecuațiile (2.2) sunt numite parametric line ecuațiilor L.

Dacă o funcție x = # 966; (t) este invers t = F (x), apoi înlocuind această expresie în ecuația y = g (t), obținem y = g (F (x)), care y definește ca funcție de x. În acest caz, spunem că ecuația (2.2) definesc funcția y parametric.

Exemplul 1. Fie M (x, y) - un punct arbitrar al unui cerc de rază R și centrată la origine. Să t - unghiul dintre axa Ox și raza OM (vezi figura 2.3.).. Dacă x, y sunt exprimate prin t:

Ecuațiile (2.3) sunt ecuațiile parametrice circumferință. Noi excludem din ecuațiile (2.3), parametrul t. În acest scop, fiecare dintre ecuațiile noi pătrat și se adaugă, obținem: x 2 + y 2 = R 2 (cos 2 t + sin 2 t) sau x 2 + y 2 = R2 - ecuația unui cerc în coordonate carteziene sistem. Aceasta definește două funcții: Fiecare dintre aceste funcții este dată de ecuațiile parametrice (2.3), dar pentru prima funcție. iar pentru a doua.

Exemplul 2. parametric ecuația

definesc o elipsă cu semi-axe a, b (fig. 2.4). Eliminarea ecuații parametru t. Noi obținem ecuația canonică a unei elipse:

Exemplul 3. cicloida numita linie punct culcat descris pe un cerc, în cazul în care acest cerc role fără să alunece pe linia dreaptă (fig. 2.5). Introducem ecuațiile parametrice ale cicloida. Lăsați raza cercului de rulare este egală cu un. punctul M. descrie cicloida, la începutul mișcării coincide cu originea.

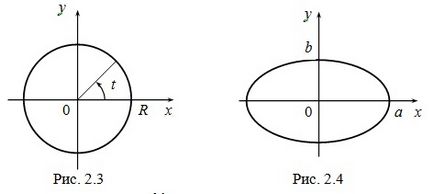
Definim coordonatele x. M punctul y după cercul de întoarcere cu un unghi t
(Fig. 2.5), t = ÐMCB. MB lungime arc egală cu lungimea segmentului OB, ca role de cerc, fără alunecare, deci

OB = la, AB = MD = Asint, CD = acost, x = OB - AB = at - Asint = a (t - sint),

y = AM = CB - CD = a - acost = a (1 - cost).

Astfel, obținut ecuațiile parametrice ale cicloidei:

Când parametrul t de la 0 până la circumferința 2π este rotită cu o rotație, punctul M descrie un arc de cicloidă. Ecuațiile (2.5) este setat ca funcție de y la x. Deși funcția x = a (t - sint) are o funcție inversă, dar nu poate fi exprimată prin funcții elementare, astfel încât funcția y = f (x) nu poate fi exprimată în termeni de funcții elementare.

Luați în considerare funcția derivare dată de ecuațiile parametrice (2.2). funcția x = # 966; (t) modificări la un anumit interval t are funcție inversă t = F (x). apoi y = g (F (x)). Fie x = # 966; (t). y = g (t) sunt derivate, în care x't ≠ 0. Conform regulii pentru diferențierea unei funcții compozit y'x = y't × t'x. Pe baza regulilor de diferențiere a funcțiilor inverse. Prin urmare:

Formula rezultată (2.6) permite găsirea derivata funcției definită parametric.

Exemplul 4. Lăsați functia y. în funcție de x. parametrizate:

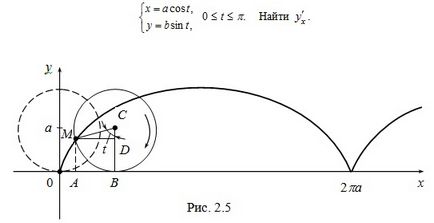
Decizie. .
Exemplul 5. Găsiți coeficientul k unghiular în tangent la punctul cicloidă M0. corespunzătoare valorii parametrului.
Decizie. Din ecuațiile cicloidale: y't = Asint, x't = a (1 - costuri), prin urmare

Panta tangentei la punctul M0 este valoarea la t0 = π / 4:

Fie funcția de la punctul x0 are un derivat. Prin definiție:
Prin urmare, proprietățile limită (Sec. 1.8). în cazul în care un - atunci când un infinitezimal # 916; x → 0. Prin urmare,

# 916; y = f „(x0) # 916; x + # 945; x # 916; x. (2.7)

la # 916; x → 0, al doilea termen din ecuația (2.7) este o infima de ordin superior, în comparație cu. prin urmare # 916; y și f '(x0) x # 916; x - echivalent infinit de mic (dacă f' (x0) ≠ 0).

Astfel, funcția de creștere # 916; y este compus din doi termeni, primul dintre care f „(x0) x # 916; x este o creștere a părții principale # 916; y, un relativ liniar # 916; x (dacă f „(x0) ≠ 0).

Funcția Differential f (x) la x0 este principala parte a funcției de creștere și notat: dy sau df (x0). Prin urmare,

df (x0) = f „(x0) x # 916; x. (2.8)

Exemplul 1. Găsiți funcția diferențială dy și funcția de creștere # 916; y pentru functia y = x 2 prin:
1) arbitrar și x # 916; x; 2) x0 = 20, # 916; x = 0,1.

1) # 916; y = (x + # 916; x) 2x 2 = x 2 + 2x # 916; x + (# 916; x) 2x 2 = 2x # 916; x + (# 916; x) 2. dy = 2x # 916; x.

2) Dacă x0 = 20, # 916; x = 0,1, atunci # 916; y = 40 x 0,1 + (0,1) 2 = 4.01; dy = 40 x 0,1 = 4.

Scriem ecuația (2.7) sub formă de:

# 916; y = dy + a × # 916; x. (2.9)

crește # 916; y diferențiale dy diferă de la o infima de ordin superior în comparație cu # 916; x, astfel încât în ​​calculele aproximative sunt aproximative egalitate # 916; y ≈ dy, dacă # 916; x este suficient de mică.

Având în vedere că # 916; y = f (x0 + # 916; x) - f (x0), obținem formula aproximativă:

Exemplul 2. Se calculează aproximativ.

Folosind ecuația (2.10), obținem:

.

Deci, ≈ 2,025.

Să considerăm df sens geometric (x0) a diferențialului (fig. 2.6).

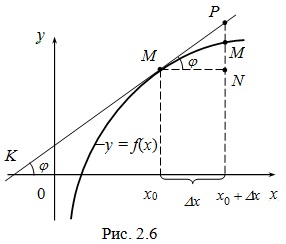
Pentru a desena un grafic al funcției y = f (x) tangentei la punctul M0 (x0, f (x0)), să # 966; - unghiul dintre tangenta și axa km0 Ox, atunci f „(x0) = tg # 966;. din # 916; M0NP:
PN = tg # 966; x # 916; x = f „(x0) x # 916; x = df (x0). Dar PN este coordoneze incremental tangenta schimbare x de la x0 la x0 + # 916; x.

În consecință, diferențiala funcției f (x) la x0 este egală cu tangenta increment ordonata.

Găsim diferențial funcției
y = x. Deoarece (x) „= 1, atunci dx = 1 x # 916; x = # 916; x. Presupunem că diferențiala variabilei x independent este egală cu increment acesteia, adică dx = # 916; x.

Dacă x - orice număr, rezultă din (2.8) obținem df (x) = „(x) dx, unde f.
Astfel, derivata funcției y = f (x) este raportul dintre diferențial la diferențiala argumentul său.

Luați în considerare proprietățile funcției diferențiale.

Dacă u (x), v (x) - funcția diferențiabilă, atunci următoarea formulă:

Pentru a demonstra aceste formule se folosesc derivați cu formula pentru suma, produsul și funcțiile private. Arătăm, de exemplu, formula (2.12):

d (u × v) = (u × v) '# 916; x = (u × v' + u '× v) # 916; x = u × v' # 916; x + u „# 916; x x v = u × v + dv x du.

Să considerăm o funcție diferențială complexă: y = f (x), x = # 966; (t), adică y = f (# 966; (t)).

că x't = dx, dy obține = y'x dx = f „(x) dx.

Astfel, funcția diferențială a unei y funcției = f (x), unde x = # 966; (t), este dată de dy = f „(x) dx, la fel ca și în cazul în care x este variabila independentă. Această proprietate este numită diferențial forma invarianta și.