grafice Euler

Simonenko EA matematică discretă. prelegeri

Ciclul Euler este un ciclu care trece pe fiecare muchie a grafului exact o dată. În consecință, graficul conține un ciclu, numit Euler. Formulați un criteriu grafic Eulerian:

Teorema (Euler, 1736.). Connected graf neorientat conține ciclu Eulerian dacă și numai în cazul în care un număr impar de vârfuri de zero grade.

Pentru o formulare grafic direcționată a teoremei este oarecum diferită: un grafic direcționat are un ciclu Euler dacă și numai dacă este conectat și gradul de fiecare nod este egal cu nivelul de intrare al producției.

Dacă există ciclu Euler în grafic, aceasta înseamnă că, urmând de-a lungul acestui ciclu, este posibil să se tragă un grafic pe hârtie, fără a ridica creionul de la ea.

Să presupunem că avem un graf neorientat G, satisfăcând Teorema lui Euler. Luați în considerare a găsi algoritm ciclu Eulerian în acest grafic. Acest algoritm se bazează pe dipozitive grafic în profunzime. În tranziția la următoarea sus va elimina o nervură corespunzătoare a călătorit. La detectarea vârfurilor de la care nervurile nu merg (le-am eliminat devreme în dipozitive adânc), va înregistra numărul său în stivă. detecție vârfuri cu zero margini sugerează că a găsit un ciclu. Acesta poate fi eliminat, iar paritatea vertex grade nu se va schimba. Procesul continuă atâta timp cât nu există margini nu traversată. După încheierea întregului grafic traversal în număr adâncime de noduri să fie stocate într-o stivă în ordinea ciclului Euler.

Conectare. Count Graph, reprezentată prin matricea de adiacență; partea de sus a stivei stiva Euler numărul ciclului de pornire vertex U.

Pentru toate nodurile V grafuri Graph, U adiacent: Graph [U, V]: = 0, graficul [V, U]: = 0; DFS (Graph, Stack, V).

Cu sarcina de a găsi cicluri hamiltoniene sunt strâns legate de problema comis-voiajor (un Hawker). Formulată în acest fel: există n orașe, distanțele dintre ele sunt cunoscute. Comerciant va vizita toate orașele n exact o dată, revenind la cel din care a început călătoria. Necesar pentru a găsi o cale pentru vânzător ambulant cu o lungime totală minimă.

Figura 3: Exemplu tetagrafa

Simonenko EA matematică discretă. prelegeri

grafice planare

Se spune că graficul este plasat pe orice suprafață în cazul în care poate fi desenată pe această suprafață, fără a trece margini. Dacă graficul poate fi plasat pe un plan, un grafic se numește plan. Contele pus pe un plan numit plat.

Zona delimitată de marginile unui grafic plană și nu conțin alte noduri și muchii ale grafului, numit o fata. Partea exterioară a planului în raport cu graficul sunt, de asemenea, considerate a fi o față. Numărul fețelor plane ale lui G este notat cu r (G).

Teorema (formula lui Euler). Într-un grafic planar conectat G = (V. E) egalitatea n - m + r = 2 unde n = V m = E și r = r (G).

Dacă G - conectat grafic planar, n> 3. 3 apoi m n - 6. Într-adevăr, fiecare față este delimitată de cel puțin trei muchii, și fiecare margine limite nu mai mult de două fețe, prin urmare, r 3 2 m. Din aceasta și din formula Euler: = 2 n - m + r n - m + 2 m / 3. În continuare: 3 n - 3 m + 2 m 6 m 3 n - 6.

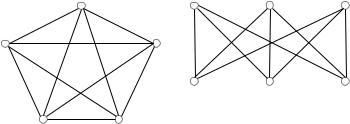
Să ne arată că K 5 și K 3,3 nu este planar. Pentru graficul K 5 avem n = 5 și m = 5, 4/2 = 10. n și m înlocuind în inegalitatea 10 3 5 - 10 9 iunie Această contradicție grafic K 5 nu pot fi plane.

Figura 4: graficele K5 și K3,3

Pentru graficul K 3,3 au n = m = 6 și 9. în acest grafic nu „triunghiuri“, astfel încât la așezarea pe planul fiecărei fețe este delimitată de cel puțin patru muchii și, prin urmare, 4 r 2 r m m 2. Conform formulei lui Euler: 6 - 9 + r = r 2 r = 5. Înlocuind în inegalitate: 05 februarie 10 09 septembrie este o contradicție.

grafic planar în care toate aspectele, inclusiv, sunt triunghiuri străine, numite

triangulare plan. grafic maxim plat este un grafic care încetează să mai fie plat, cu adaos de orice margine.

Teorema. Count este maxim plat dacă și numai dacă este plană triangulare.

Pentru fiecare grafic planar maximă, egalitatea m = 3, n - 6.

Coperta și independența

Ei spun că vârful graficului acoperă incidentul coaste la, și un incident de margine să-l acoperă partea de sus. Acest lucru ridică două probleme: 1) caută numărul minim de noduri, acoperind toate muchiile grafului G (acoperirea numărului vertex 0 α (G)); 2) găsi numărul minim de muchii, acoperind toate nodurile G (numărul de acoperire costal

Pentru complet grafic K n:

α 0 (K n) = n - 1. α 1 (K n) = [n 2]. (În cazul în care [] desemnează "plafon".)

Setul de vârfuri ale unui graf G se numește independentă. în cazul în care nu există două noduri din set nu sunt adiacente. Cel mai mare număr de noduri din setul independent este numit

vertex număr independență β 0 (G). și o multitudine corespunzătoare de cele mai mari. Setul de muchii neadiacente ale unui graf G se numește independent. Cel mai mare număr de muchii din setul independent de numărul liniei numite β independență 1 (G).

Pentru complet grafic K n:

α 0 (K n) = n - 1. β 1 (K n) = [n 2]. (În cazul în care [] desemnează "podea".)

Teorema. Pentru orice grafic fără vârfuri izolate egalitati:

alfa 0 + β 0 = n = a 1 + β 1.