Mișcarea unei particule încărcate într-un câmp magnetic și electric

Partea 3: Electricitate și Magnetism

Secțiunea 9 din magnetism. DOMENIUL MAGNETIC ENERGIEI ELECTRICE

9.6. Mișcarea unei particule încărcate într-un câmp magnetic și electric. forța Lorentz

Un conductor prin care trece curent este diferit de conductorul de curent, fără ca acesta să provină deplasarea ordonată a purtătorilor de sarcină. Acest lucru sugerează că forța care acționează asupra conductorului parcurs de curent plasat într-un câmp magnetic datorită acțiunii forțelor asupra sarcinilor în mișcare individuale. Și deja prin acțiunea acestor taxe este trecut un conductor prin care se mișcă. Această abordare face posibilă determinarea forței care acționează asupra unei sarcini separate, care se mișcă într-un câmp magnetic. Aceasta se numește forța Lorentz.

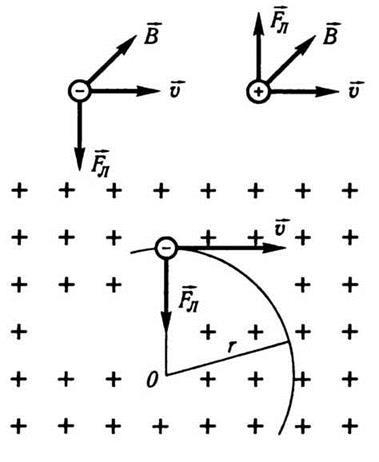
Să presupunem că o viteză de electroni având. Ea zboară într-un câmp magnetic uniform de inducție B așa cum se arată în Fig. 9.7. Liniile de inducție magnetică și marcat Crucea dirijată din cititorul perpendicular pe planul figurii. O particulă încărcată în mișcare este un microcurrent electric. Apoi, pentru a determina forța cu care acționează de câmp magnetic pe o taxa de e în mișcare (e - taxa de electroni), puteți utiliza legea Amperi. Conform legii lui Ampere la curent l rectiliniu câmp magnetic uniform cu element de inducție acționează cu o forță α IlBsin egale [Formula (9.21)] (α - unghiul dintre câmpul și curent). Să taxa în mișcare e într-un timp t este deplasat cu o distanță L. Acest lucru este similar cu elementul curent, a cărui putere I =. Substituind această expresie în formula (9.21), obținem l Bsin α. Având în vedere că, în acest caz, păcatul α = l și l / t = υ. în cele din urmă obținem expresia forței Lorentz:

Pentru a determina direcția forței Lorentz poate fi aplicat manual, în general, la stânga. Cu toate acestea, în acest caz, degetele ar trebui să fie plasate, nu în direcția de mișcare a electronului, și împotriva mișcării sale, din moment ce electronul este încărcată negativ, iar pentru direcția direcției curente luate sarcini pozitive. Folosind conceptul de produs vectorial, formula (9.26) poate fi scrisă sub forma:

Apoi, (9.27), în același timp, pentru a determina valoarea și direcția forței care acționează într-un câmp magnetic pe un electron în mișcare. Direcția de forța care acționează în câmpul magnetic asupra particulei încărcate pozitiv, coincide cu direcția produsului vector, [], adică

Formulele (9.27) și (9.28) pot fi combinate

dar trebuie să se înțeleagă prin valoarea algebrică q a taxei care se misca (q> 0 pentru sarcini pozitive și q 0 pentru negativ). Fig. 9.7 arată pozițiile relative ale vectorilor L. Pentru sarcini pozitive și negative.

Deoarece forța Lorentz L este întotdeauna perpendicular pe viteza particulei încărcată, aceasta nu efectuează lucrarea, ci doar schimbă direcția de mișcare a unei particule încărcate într-un câmp magnetic. Valoarea absolută a vitezei particulelor încărcate și energia cinetică nu sunt modificate. Lorentz forță este forța centripetă și oferă o particulă încărcată, accelerația centripetă este egală. în cazul în care v - viteza de mișcare a electronului; r - raza de curbură a traiectoriei de electroni într-un câmp magnetic. Apoi, utilizând vectorii perpendiculare i. scrie

în care q - taxa particulei; m - masa acesteia.

Formula (9.30) arată că traiectoria particulei încărcată care intră în câmpul magnetic uniform (a = const), la un unghi față de liniile de inducție magnetică și are aceeași curbură este deci un cerc cu raza, pornind de la ecuația (9.30) este egal cu

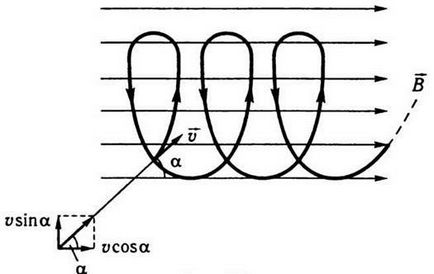
Dacă un spațiu în care particula încărcată în mișcare pentru a crea un unghi de câmp napryamlene magnetic α la viteza, atunci mișcarea particulei poate fi considerată ca o sumă geometrică a celor două mișcări au loc simultan, și anume rotația într-un cerc, la o viteză υ α sin în plan, perpendicular pe liniile, și se deplasează de-a lungul câmpului cu o viteză υ cos α. În consecință, traiectoria particulei, în acest caz, ia forma unei elice a cărei axă este paralelă cu direcția vectorului (fig. 9.8).

Efectul câmpului electric asupra mișcării unui electron sau alte particule încărcate diferă substanțial de influența câmpului magnetic. Câmpul electric modifică energia cinetică a electronului, în timp ce câmpul magnetic schimbă doar direcția, dar nu viteza. Mișcarea particulelor încărcate, cum ar fi electroni într-un câmp electric este în general similar cu mișcare a corpului într-un câmp gravitațional: dacă viteza inițială a electronului este opusă direcției liniilor de forță ale unui câmp electric omogen, forța care acționează asupra coincide cu direcția vitezei - electron se mișcă rіvnopriskoreno. În direcția inversă se va muta rіvnospovіlneno viteza. Dacă viteza inițială a electronului este perpendicular pe direcția liniilor de câmp ale câmpului electric omogen, electronul va descrie o parabolă.

Forța exercitată de câmp electric uniform pe un electron, care intră în ea perpendicular pe liniile de tensiune numai la momentul inițial este centripetă. În consecință, raza de curbură r a electronului la punctul de pornire al parabolei poate fi calculată din raportul

unde E - câmp electric; m - masa electronului. Astfel, electronii deviante câmp electric transversal, raza de curbură a căii este proporțională cu pătratul vitezei:

În cazul general, mobil de încărcare q electric poate funcționa simultan cu inducerea câmpului magnetic și intensitatea câmpului electric este caracterizat. Apoi, forța rezultantă. care acționează asupra taxa este egală cu suma vectorială a forțelor f = q. care funcționează pe o taxă de câmp electric și forța Lorentz L = q [,]:

Această expresie se numește formula Lorentz. Conform (9.31) la o deviere a unui câmp magnetic de electroni, raza de curbură a traiectoriei sale este proporțională cu viteza. Această funcție este utilizată pentru a măsura viteza de electroni prin compensarea reciprocă a acțiunii câmpurilor electrice și magnetice pe mișcarea de electroni.

Plasarea Polii plat al electromagnetului, astfel încât liniile câmpului magnetic sunt perpendiculare pe liniile de forță ale câmpului electric și fluxul de electroni trecut simultan între polii electromagnetului și condensator planul plăcii, reglarea curentului în electromagnetului înfășurare (schimbare de inducție câmp magnetic), devierea electronilor de la liniar cale, indus de câmpul electric, poate fi compensat integral de aceeași valoare, dar opusă direcție devierea provocată de câmpul magnetic. Din formulele de razele de curbură a traiectoriei electronilor într-un electric transversal (9.33) și (9.31), câmpurile magnetice se poate observa că abaterea poate fi compensată reciproc pentru

sau relația

Această formulă permite determinarea vitezei particulelor incarcate (electroni) care măsoară inducția câmpului electric și magnetic, alese astfel încât acțiunile lor sunt kompensuvalis reciproc articulate. Dacă, ulterior, eliminarea câmpului electric și se măsoară deformarea electronilor în câmpul magnetic, apoi la r. E și B poate determina încărcătura specifică a electronului - raportul dintre sarcina electronului la masa. Formula de calcul a acestui raport poate fi obținut din (9,31) și (9.35):

Taxa specifică a electronului a fost definit mai întâi de George. Thomson. Pe baza măsurătorilor în deformarea electrică și câmpuri magnetice de raze catodice, sa constatat că

Având în vedere că taxa elementară e = 1,602 ∙ 10 - CI 19, și cunoașterea e / m. constatăm că masa m electroni = 9,109 ∙ 10 -31 kg.

O metodă de determinare e / t, poate fi utilizată atunci când toate particulele din fluxul au aceeași viteză. Toți electronii care formează un fascicul, accelerat de același potențial diferență care este aplicată între catod din care sunt emise, iar anodul; Prin urmare, se împrăștie vitezele de electroni în fluxul este foarte mic.

ionii pozitivi sunt formate prin ionizare a moleculelor de gaz. Care apar în locuri diferite, diferiți ioni a depăși diferența de potențial, prin care viteza de diverși ioni diferă unul de altul. Prin urmare, metoda prin care taxa specifică a electronului, sa determinat să nu fie aplicată ionilor.

În 1907, George. Thomson a dezvoltat o „metoda de parabole, cu care se poate determina taxa specifică a ionilor.

. Efectuarea experimentului cu neon chimic pure, iar J. Thomson a constatat că acest gaz formează un parabole două mase atomice 20 și 22. încercările de a explica acest rezultat a condus la presupunerea că există două tipuri de atomi de neon chimic indivizibile corespunzătoare (în terminologia modernă - doi izotopi de neon) . F. dovedit această presupunere Aston, care sa îmbunătățit metoda de determinare a taxei specifice a ionului. Dispozitiv prin care poate fi determinată de e / m de diverși ioni, F. Aston numit spectrograf de masă.