pendulului de primăvară, și exemple de formula
pendul de primăvară - un sistem vibrator care constă din punctul de masă și un arc (Fig.1).
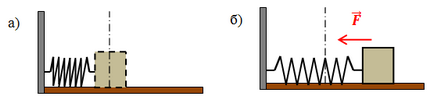
Fig.1. pendul Spring: a) în poziția de echilibru; b) capabil să vibrații
Când arcul nu este deformat, corpul este într-o stare de echilibru (Figura 1 a). În cazul în care se întinde sau comprimarea arcului, pentru a aduce corpul din poziția sa de echilibru, acesta va forța care acționează din arcul elastic deformate. Această forță este îndreptată spre poziția de echilibru, și în acest caz, este forța de revenire.
forța elastică într-un pendul de primăvară
forță proporțională elastică a corpului de deplasare (arc alungire):
aici - constanta de primăvară.
Într-o poziție care corespunde la deformarea maximă a corpului, de la poziția de echilibru (corp offset este amplitudinea oscilației) este forța elastică maximă și, prin urmare, accelerația maximă a corpului. Deoarece corpul se apropie de poziția de echilibru a descrește alungire de primăvară, și, prin urmare, accelerarea corpului scade, care este cauzată de forța elastică. După ce a ajuns în poziția de echilibru, organismul nu se va opri, cu toate că în acest moment forța arcului este zero. viteza corpului la momentul trecerii sale prin poziția de echilibru are o valoare maximă, iar corpul de inerție va merge mai departe, care se întinde arcul. Forța de elasticitate va încetini corpul, pentru că acum este îndreptată în direcția opusă mișcării corpului. După atingerea poziției extreme, corpul se oprește și începe să se miște în direcția opusă. Mișcarea corpului se repetă în secvența descrisă.
Astfel, provoacă vibrații arcului pendulului este deformată elastic forța arcului (forță de revenire) și corpul de inerție.
Perioada de oscilație liberă a arcului pendul
Perioada de oscilație liberă a arcului pendulului este determinată prin formula: