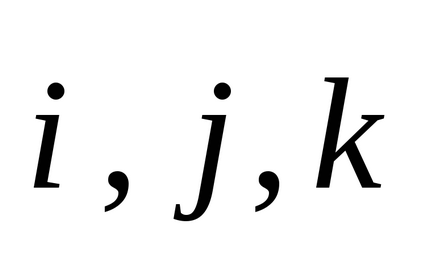Produsul dot a doi vectori și proprietățile sale

Definiția. produsul scalar a doi vectori

șieste un număr egal cu produsul modulelor de vectorișicosinusul unghiului dintre ele.

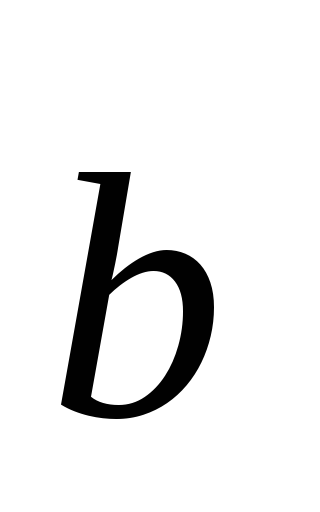
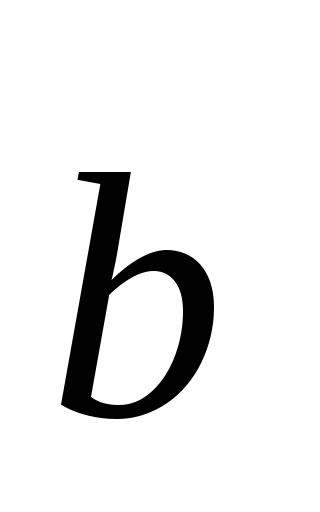
Produsul scalar a doi vectori

șireprezenta, sau.

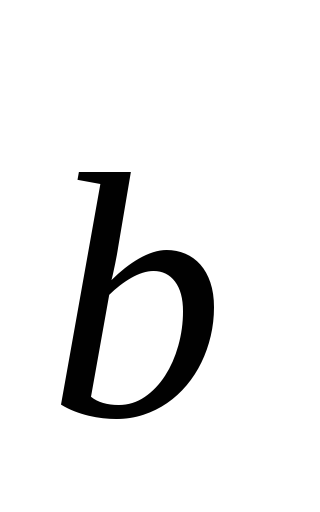
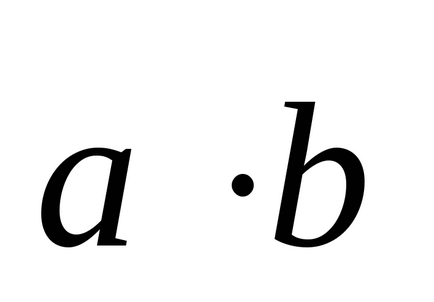
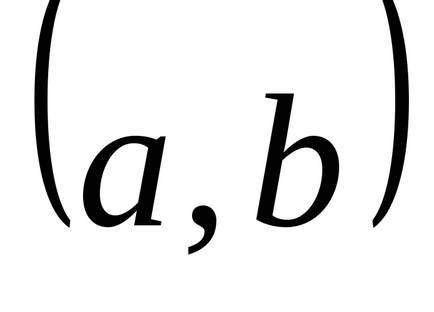
Deci, prin definiție,

,

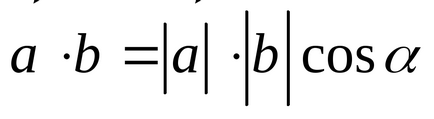
unde

- unghiul dintre vectoriică.

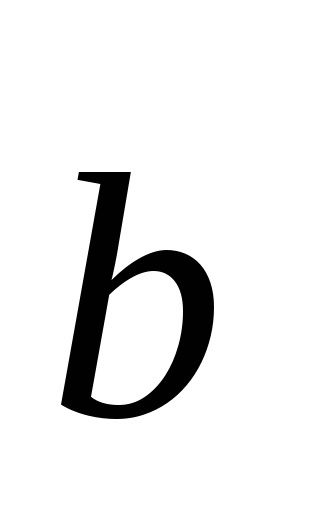
Dacă cel puțin unul dintre vectorii este zero, atunci unghiul nu este definit și produsul scalar prin definiție este considerată a fi zero.

Deoarece formula

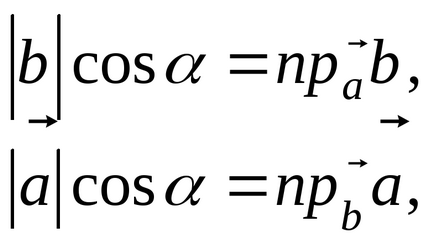
produsul scalar cu formula poate fi scrisă, astfel:

.

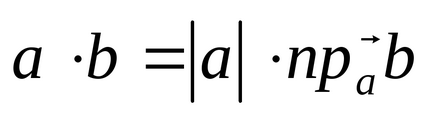
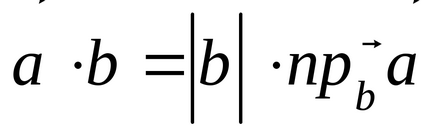
Astfel, produsul scalar a doi vectori este egal cu produsul din modulul vectorilor pe o proiecție al doilea vector pe prima.

produsul scalar are următoarele proprietăți:

produsul 1.Skalyarnoe este comutativă, adică, pentru orice vectori

. (2.14)

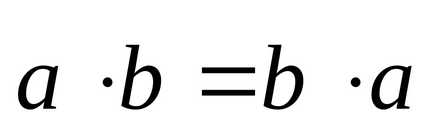
2, și anume pentru un vector arbitrar al pătrat sale scalare este egală cu pătratul unității vector. aici

. (2.15)

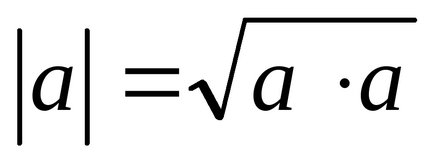
3. Produsul scalar este egal cu zero dacă și numai dacă factorii sunt ortogonale, sau cel puțin unul dintre ei este zero.

4. Produsul scalar este asociativă în raport cu un factor de scalare, adică. (2.16)

5. distributivă produsului scalar în ceea ce privește adăugarea, adică pentru oricare trei vectori

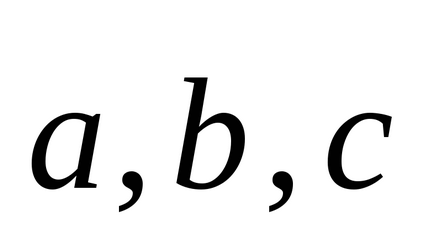
avem egalitatea

.

6. ortonormate vectori de bază satisfac relațiile:

,

.

Să considerăm acum doi vectori

și, care stabilește coordonatele într-un sistem de coordonate cartezian:;,

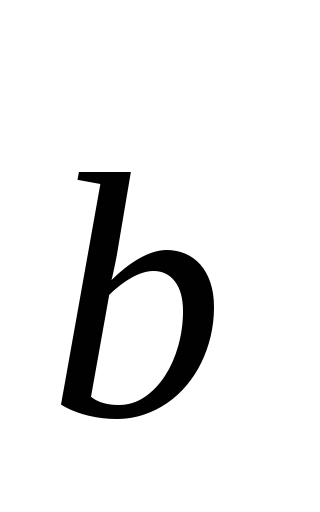
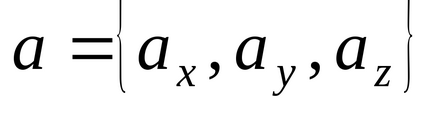
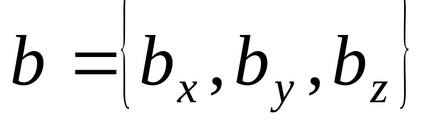
Apoi, folosind proprietățile de mai sus ale produsului scalar, obținem

, produs scalar a doi vectori într-o bază ortonormală este suma lucrărilor coordonatelor lor respective.

, Modulul vector este rădăcina pătrată a sumei pătratelor coordonatelor.

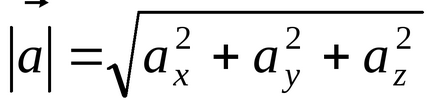
Cosinusul unghiului dintre cei doi vectori

.

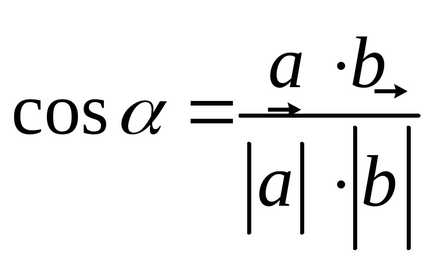
Pentru a obține baza ortonormală:

și ortogonalitatea a doi vectori devine :.

Produsul vectorial a doi vectori, proprietățile sale

Definiția 2.21. Vector produs al vectorului

un vectorEste un vector(Figura 2.15.) În care: 1) lungimea este numeric egală cu aria paralelogramului construit pe acești vectori.

2) vectorul perpendicular pe planul în care vectoriiși, și anumeși;

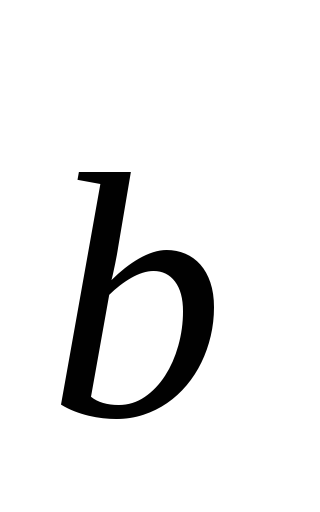
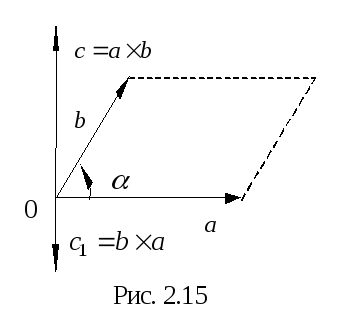
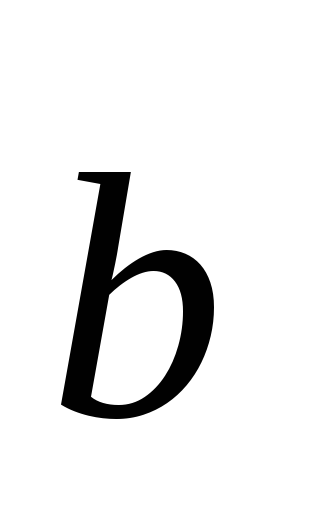
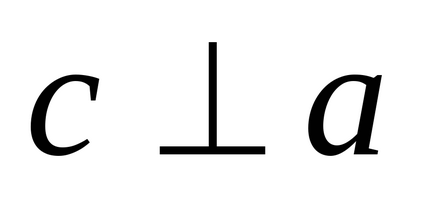
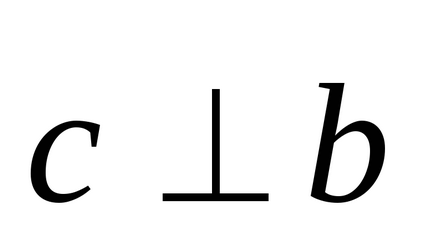
3) vectorul

Acesta este direcționat astfel încât să se transforme pe cel mai scurt vectorla vectorulefectuat în sens antiorar când este privit din capătul vectorului.

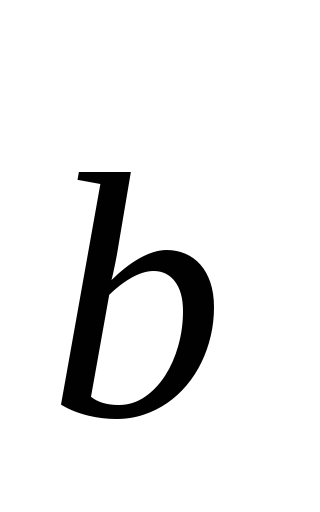
produs Vector

șinotatsau.

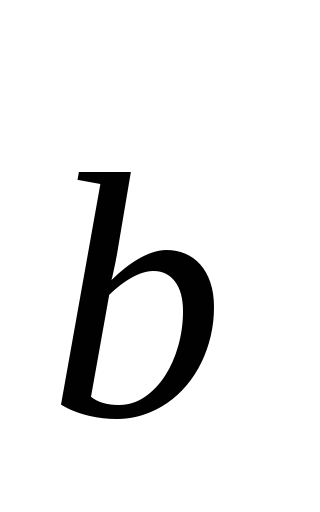
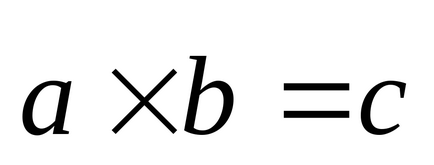
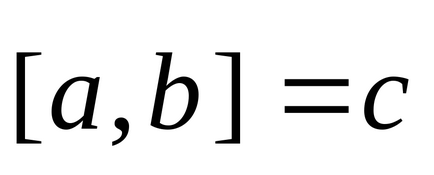
Din definiția rezultă că proprietățile:

2) - asociativitatea multiplicator scalare;

3) - împărțire peste plus;

4)

Este vectori coliniareși.

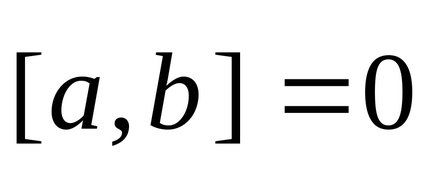
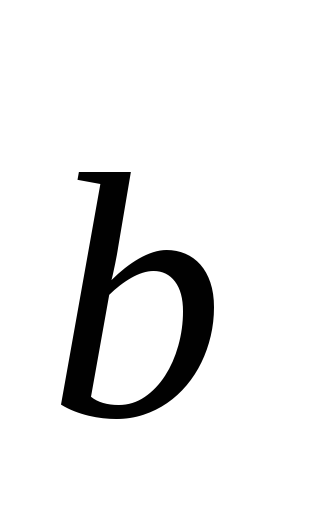
Pentru ca produsul vector de bază al versorii

deține un astfel de tabel (Tabelul 2.1).