Provocări pentru calcularea suprafeței diferitelor tipuri de polihedre
Provocări pentru calcularea suprafeței diferitelor tipuri de polihedre
Setarea 8_1. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
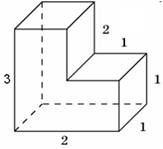
Suprafața unui poliedru poate fi calculată ca suma ariilor fețele sale. În care suprafața fețelor frontale și posterioare sunt
iar întreaga suprafață este
Setarea 8_2. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
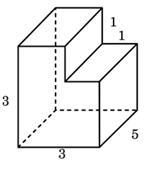
Gasim aria suprafeței ca suprafața unui paralelipiped dreptunghic cu laturile 3, 3, 5 și scade pătrat 1x1 două fețe ale unui paralelipiped dreptunghic cu laturile 1, 1 și 3 (a se vedea. Figura).
Suprafața unui paralelipiped mare este
Piața se confruntă cu două mici 1x1 paralelipipedică, sunt:
și suprafața figurii
Setarea 8_3. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
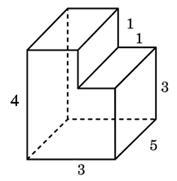
Figura arată că formele din zona de suprafață va fi mai mică decât aria unui paralelipiped dreptunghic cu laturile 3, 4 și 5 pe suprafața celor două pătrate de dimensiune 1x1, avem:
Setarea 8_4. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
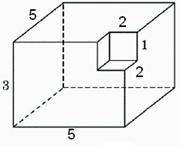
Se poate observa că suprafața figurii va fi exact la fel ca și suprafața unui paralelipiped dreptunghic cu laturile 5, 3 și 5 și este egal cu
Notă. A nu se confunda calcularea volumului figurii și aria suprafeței sale!
Setarea 8_5. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
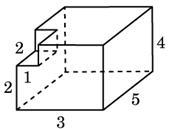
Suprafața acestei figuri este suprafața unui paralelipiped dreptunghic cu laturile 3, 4 și 5, și este egală cu
Notă. A nu se confunda calcularea volumului figurii și aria suprafeței sale!
Setarea 8_6. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
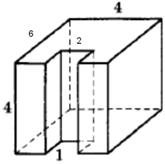
Suprafața această cifră poate fi calculată ca suprafața unui paralelipiped dreptunghiular cu laturile de 4, 4 și 6, plus două fețe zonă 1x4 4 (a se vedea. Figura) și minus două fețe pătrat 2x1 (ele se scad din baza). Astfel, zona este cifra
Setarea 8_7. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
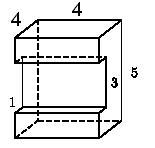
Pătratelor fețelor inferioare și superioare ale zonei egală a fețelor laterale pot fi calculate ca zona muchiilor frontale și posterioare, respectiv, și mai necesar să se ia în considerare două zone din interiorul fețele superioare și inferioare. Astfel, întreaga suprafață a figurii este
Setarea 8_8. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
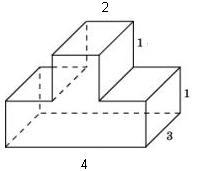
Formele de suprafață specifică poate fi calculată ca suprafața unui paralelipiped dreptunghiular cu laturile de 4, 3 și 2, minus patru pătrate pătrate laterale 1x1. Avem:
Setarea 8_9. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
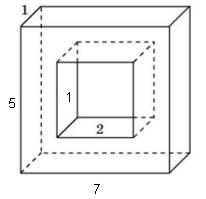
Figura prezintă un paralelipiped dreptunghiular cu tăietură. Suprafața figurii va fi egală cu întreaga suprafață a unui paralelipiped cu laturile 5, 7 și 1 minus două zona adâncitură frontală a zonei de 2x1 = 2 și plus patru laturi interioare ale zonei decupaj dimensiunile 1x1 și 2x1. Astfel, întreaga suprafață a poliedrului este egală cu
Setarea 8_10. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
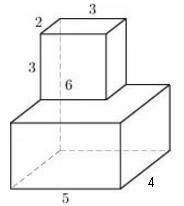
Suprafața unui poliedru poate fi găsită ca o sumă de pătrate de două paralelipiped dreptunghic cu laturile de 5, 4, 3, 3, 2, 3 minus două paralelipiped inferioare din zona de bază pătrată de 2x3 (două zone, deoarece este considerată în două paralelipipede mari și mici) . Astfel, obținem:
Setarea 8_11. Găsiți o suprafață poliedru prezentată în figură, toate unghiurile drepte diedru.
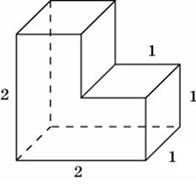
Găsim suprafața figura ca zona a unui paralelipiped dreptunghic cu laturile 2, 2, 1, și scade cele două fețe ale pătrat 1x1 în planuri frontale (față și spate), obținem:
Setarea 8_12. Găsiți o suprafață spațială a crucii prezentat în figură și este compus din cuburi de unități.
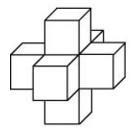
Aria suprafeței a figurii poate fi găsită ca suma suprafețelor de 6 cuburi minus suprafața unui cub (unul în interiorul și în aceste fețe nu sunt incluse în zona de suprafață), obținem:
Setarea 8_13. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
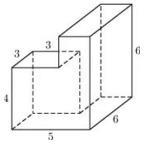
Considerăm că zona de suprafață a unui poliedru ca suma suprafețelor mari (6h6h2) și (3h3h4) cuboizi mici și scade de două ori suprafața fețelor de contact ale paralelipipede, care are o dimensiune de 3x4, obținem:
Setarea 8_14. Găsiți o suprafață poliedru prezentată în figură (toate unghiurile diedre sunt unghiuri drepte).
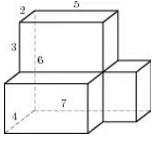
Suprafața unui poliedru poate fi găsită ca o sumă de zone de suprafață ale fiecăreia dintre cele trei dimensiuni 2h5h6 paralelipipede și 2h5h3 2h3h2 minus dublul ariei de contact a acestor paralelipipede, adică minus de două ori zona dintre cele două fețe de dimensiuni 3x5 și 2x3 respectiv. Rezultatul este o suprafață a figurii:
Setarea 8_15. Prin midline triunghiular plan de bază prismă a avut loc paralel cu marginea laterală. Găsiți aria suprafeței laterale a prismei dacă suprafața laterală este întreruptă printr-o prismă triunghiulară 37.
Deoarece planul secțiunii transversale tras prin linia de mijloc, se împarte în jumătate din planul lateral. În consecință, o mai mare suprafața laterală a prismei de 2 ori mai mare suprafață laterală este mică și prismei 74.