Raza cercului, diametrul, pi, sector, tangenta

Raza. distanta de la centrul cercului la marginea sa.

Diametru. cea mai mare distanță de la o margine circumferențială la alta. Diametrul este de două ori raza.

Perimetru (circumferința). Circumferința de frontieră.

Circumferința $ = \ pi \ ori $ diametru

Doug. o linie curbă, care face parte din cercul.

Arc măsurată în grade sau radiani. De exemplu: 90 °, sau $ \ frac $ - sfert de cerc, 180 ° sau $ \ pi $ - jumătate din cerc.
Suma tuturor arcurilor este de 360 ​​°

Coardă. un segment de linie care leagă două puncte de pe cerc.

Sectorul. ca o bucată de tort (pană).

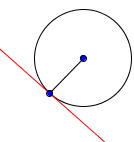
Tangenta la cercul: linia dreaptă perpendicular pe raza, și având un singur punct în comun cu okurzhnostyu.

Circumferința $ = \ pi \ cdot \ text = 2 \ cdot \ pi \ cdot \ textul $

Gama zona de cerc $ = \ pi \ cdot $ cu 2

Raza notată r. ca diametrul d. P ca circumferința și suprafața ambelor S.

$ P = \ pi \ cdot d = 2 \ cdot \ pi \ cdot r $
$ S = \ pi \ cdot r ^ 2 $

Zona unui sector de cerc, K. (cu unghi central de $ \ theta $ și raza $ r $).
Dacă unghiul de $ \ theta $ în grade, atunci zona = $ \ frac \ pi r ^ 2 $
Dacă unghiul de $ \ theta $ în radiani, atunci zona, apoi zona = $ \ frac r ^ 2 $

În cazul în care lungimea arcului este de $ \ theta $ clasificare sau radiani, valoarea unghiului centrale ca $ \ theta $ (grade sau radiani).

(. În inci, curti, picioare, inci, metri) Dacă cunoașteți lungimea arcului puteți găsi valoarea sa corespunzătoare unghiului central ($ \ theta $), folosind formula:

unghiul înscris

Unghiul Inscripționată este un unghi cu vârful pe circumferință și cu laturile care conțin coarda cercului.
În figură, unghiul de APB este inscripționată unghi.

Valoarea unghiului înscris este jumătate din arc pe care se bazează.

exemplu:
$ \ Widehat = 84 ^ \ $ Circ
$ \ Unghi APB = \ frac = 42 ^ \ $ Circ

Cazul 1: cele două secants se intersectează în interiorul circumferinței.

Când două secants se intersectează în interiorul cercului, valoarea unghiului format de două ori mai puțin decât valorile arcele pe care se bazează. Figura arc arc AB și CD sunt 60 ° și 50 ° în timp ce unghiurile 1 și 2 sunt egale cu $ \ frac (60 ^ \ ^ 50 + Circ \ Circ) = 55 ^ \ $ Circ

Cazul 2: două de intersecție se intersectează în afara cercului.

Uneori, secants se intersectează în afara cercului. Când se întâmplă acest lucru, mărimea unghiului rezultat este egal cu jumătate din diferența dintre arce pe care se bazează.

$ \ Unghi ABC = \ frac (x - y) $

Figura de arc AB = 80 ° și CD-arc = 30 °.
$ \ Unghi ABC = \ frac (80 - 30) = \ frac \ cdot 50 = 25 ^ \ $ Circ

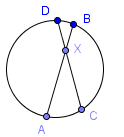
Dacă două acorduri se intersectează în interiorul circumferință, așa cum se arată mai sus, atunci:

$ AX \ cdot XB = CX \ cdot XD $