site-ul personal - cerc numeric
cerc numeric
Cerc numeric - este cercul unitate, ale căror puncte corespund anumitor numere reale.
Cercul unitate este cercul de rază 1.
Vedere de ansamblu circumferința numerică.
1) Raza sa este luată ca unitate.
2) Diametrele orizontale și verticale ale cercului numeric împărțit în patru sferturi (a se vedea figura). Acestea sunt denumite, respectiv primul, al doilea, al treilea și al patrulea trimestru.
3) Diametrul orizontal desemnat AC și A - este punctul cel mai din dreapta.
Notăm diametru vertical BD, iar B - este punctul superior extremă.
În consecință:
În primul trimestru - acest arc AB
al doilea trimestru - BC arc
al treilea trimestru - arc CD
al patrulea trimestru - arc DA
4) Punct de plecare circumferința numerică - punctul A.
Citirea pe cercul numeric poate fi realizată atât în sensul acelor de ceasornic și invers acelor de ceasornic.
Numărarea de la punctul A în sens antiorar numit direcția pozitivă.
Numărarea de la punctul A în sens orar se numește direcția negativă.
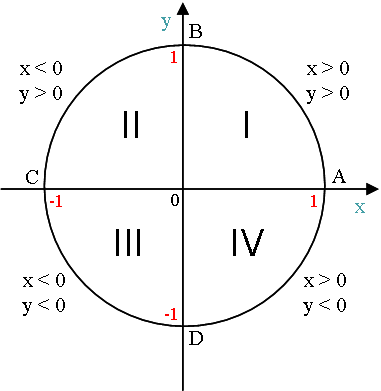
raza cercului numeric Center corespunde originii (de la 0).
Diametrul orizontală corespunde axei x. vertical - axa y.
Punct de plecare O numeric circumferential situat pe axa x și are coordonatele (1, 0).
Numele și localizarea principalelor puncte ale cercului real:
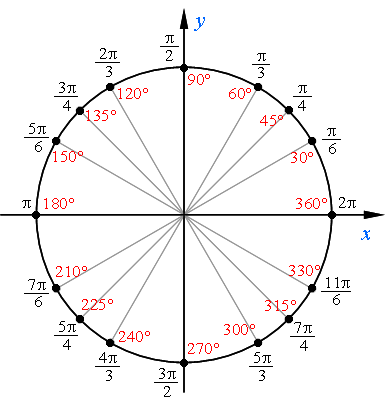
Cum să-și amintească numele cercului numeric.
Există câteva reguli simple care vă vor ajuta să vă amintiți cu ușurință numele cercului numeric principal.
Înainte de a începe, ne amintim, de numărare în direcția pozitivă, adică, de la A (2π) invers acelor de ceasornic.
1) Pentru a începe cu puncte extreme pe axele de coordonate.
Punct de pornire - este 2π (punctul cel mai din dreapta pe axa x este egal cu 1.).
După cum știți, 2π - este lungimea circumferinței. Prin urmare, jumătate din circumferința - un 1π sau π. axa x împarte circumferința de doar jumătate. Prin urmare, punctul cel mai din stânga pe axa x. este egal cu -1, numită π.
punctul cel mai de sus pe axa y. egal cu 1, împarte jumătatea superioară semicerc. Deci, în cazul în care un semicerc - este pi, apoi jumătate din semicercului - este π / 2.
În același timp, π / 2 - acesta este un sfert de cerc. Contăm trei sferturi din prima la a treia - și vom ajunge la cel mai adânc punct de pe axa y. egală cu -1. Dar, în cazul în care include trei sferturi - de aici și numele 3π / 2.
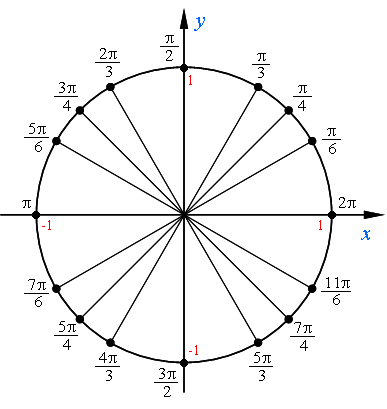
2) Ne întoarcem acum la celelalte puncte. Notă: Toate punctele opuse au aceeași numărătorul - și acesta este punctul opus și în raport cu axa y. și în raport cu axa centrală, iar x. Acest lucru ne va ajuta să știe valorile lor puncte fără buchereala.
Este necesar să ne amintim doar valoarea primelor puncte trimestru: π / 6, π / 4 și π / 3. Și apoi vom „vedea“ unele modele:
- În ceea ce privește punctele de axa y în al doilea trimestru, vizavi de primele puncte trimestru, numerele din numărătorii 1 de mai jos valorile numitorii. De exemplu, să ia punctul de π / 6. Punctul său opus în raport cu axa y, de asemenea, are 6 la numitor și în numărătorul 5 (1 mai puțin). Acesta este numele acestui punct: 5π / 6. Punctul opus π / 4, de asemenea, are un 4 la numitor și în numărătorul 3 (1 mai puțin de 4) - adică un punct 3π / 4.
Punctul de tt / 3 opus, de asemenea, are o numitorul 3 și în numărătorul este mai mic de 1: 2π / 3.
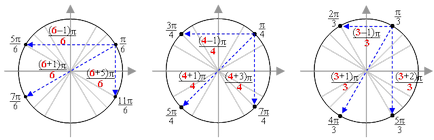
Punctul opus punctului de π / 4, de asemenea, are un 4 la numitor și în numărul numărătorul mai mare de 1: 5π / 4.
Punctul opus punctului de π / 3, de asemenea, are o numitorul 3 și în numărul numărătorul mai mare de 1: 4π / 3.
- Comparativ cu axa x (al patrulea trimestru), cazul este mult mai complicat. Aici este necesar să se adauge valoarea numitorul numărul care este mai mică de 1 - iar această sumă va fi egală cu porțiunea numerică a numărătorul contrariul. Incepem din nou cu π / 6. Adăugați la valoarea numitor egal cu 6, un număr care este 1 mai mică decât numărul respectiv - adică 5. obține: 6 + 5 = 11. Prin urmare, opusul cu privire la punctul axa x va fi de 6 la numitor și în numărătorul 11 - adică 11π / 6.
π / 4 puncte. Adaugam la valoarea numitorul numărului mai mic de 1: 4 + 3 = 7. Prin urmare, opusul cu privire la punctul axa x are 4 la numitor, numărătorul și 7 - adică 7π / 4.
π / 3 puncte. Numitorul este 3. Adaugam la unitatea 3 la numărul minim - adică obținerea 2. 5. Prin urmare, punctul său opus are un numarator 5 - și acest punct 5π / 3.
3) Un alt model pentru mijlocul patrulea punct. Este clar că numitorul lor este 4. Acordați atenție numărătorii. Numărătorul de la mijlocul primului trimestru - un 1p (1, dar nu este acceptat să scrie). Numărătorul de la mijlocul celui de al doilea trimestru - este 3π. Numărătorul mijlocul al treilea trimestru - un 5π. Numărătorul de la mijlocul celui de al patrulea trimestru - un 7π. Se pare că numărătorilor mijlocul trimestrului - primele patru numere impare în ordine crescătoare:
(1) π, 3π, 5π, 7π.
De asemenea, este foarte ușor. De la mijlocul tuturor sferturi sunt în numitorul 4, știm deja numele lor complet: tt / 4, 3π / 4, 5π / 4, 7π / 4.
Caracteristici cerc numeric. O comparație cu linia numărul.
După cum știți, pe o linie număr, fiecare punct corespunde unui număr unic. De exemplu, în cazul în care punctul A de pe linia este egal cu 3, acesta poate să nu fie egal cu orice alt număr.
La numărul de cerc este diferit, deoarece este un cerc. De exemplu, de la punctul A la cercul ajuns la punctul M, putem face ca o linie dreaptă (imediat după trecerea arcului), dar puteți merge în jurul valorii de întregul cerc, și apoi vin la un punct M. Concluzie:
Să punctul M este egal cu numărul de unele T. După cum știm, circumferința este egală cu 2p. Deci, punctul de cerc t poate fi scris în două moduri: t sau t + 2π. Această valoare echivalentă.
Adică, t = t + 2π. Singura diferență este că, în primul caz, ați ajuns la punctul M dintr-o dată, fără a face un cerc, iar în al doilea caz ați făcut un cerc, dar în cele din urmă sa dovedit a fi la același punct M. Aceste cercuri pot fi trase două, și trei, și două sute . Dacă notăm numărul de ture cu litera k. obținem o nouă expresie:
t = t + 2πk.
Dacă punctul M este numărul de numeric circumferință t, atunci este egal cu numărul și tipul t + 2πk. unde k - orice număr întreg: