teoria grafurilor definiții de bază

Teoria grafurilor - o ramură a matematicii utilizate în informatică și programare, economie, logistică, chimie.

Ce este Earl

De multe ori pentru a descrie structura sistemelor folosind organigrame. Elemente reprezinta cercuri, puncte, piețe, etc. și legăturile dintre elementele - .. Linii sau săgeți. În acest caz, nici modul în care elementele sunt afișate, nici lungimea sau forma liniilor nu este importantă - aspecte care numai elementele sunt conectate. Deci, Earl - o pereche de forma (A, M), unde A - un set finit de noduri, și M - set de margini - linii care leagă unele dintre nodurile.

Concepte de bază ale teoriei graficului

Într-un grafic sau digraph direcționată (vezi. Figura de mai jos) rib orientate, numite arcade și sunt reprezentate prin săgeți. Arcul poate fi definit printr-o pereche ordonată de noduri care se conecteaza, - la început și de sfârșit.

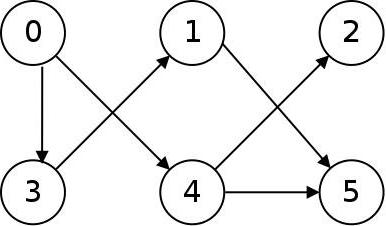
Într-un graf neorientat (vezi. Figura de mai jos) sunt reprezentate prin linii fără orientare margine. În consecință, perechea de noduri, care conectează nervura este dezordonat. Ambele aceste vârfuri au capetele coaste.

În cazul în care nodurile a și b - costale capete (sau începutul și sfârșitul arcului) a graficului, atunci spunem că nodurile A și B sunt incidente această margine (arc), și o muchie (arc) este incident de la vârfurile a și b. În cazul în care nodurile a și b - capetele nervurilor, acestea sunt (a și b) a spus să fie adiacente.

grafice Cel mai adesea considerate, ale căror margini au un tip - sunt orientate sau nu.

Dacă marginile au același început și la sfârșit, acestea sunt numite muchii multiple, un grafic în care sunt prezente, se numește multigraf.

Teoria graficul utilizează, de asemenea, termenul „buclă“ - margine merge și setarea în același top. Grafic în care există o buclă, numit pseudographs.

Cele mai frecvente grafice neorientate, care nu au mai multe margini și nici bucle. Aceste grafice sunt numite ordinare. Ei nu au mai multe margini, astfel încât să puteți identifica nervura și perechea corespunzătoare de noduri.

Fiecare nod al unui digraph se caracterizează prin:

• Jumătate-un rezultat. Acesta este numărul de arce care derivă din acesta.
• Indegree. Acesta este numărul de arce, care sunt incluse în acest summit.

Suma de digraph indegree, iar suma outdegree egal cu numărul total de arce.

Într-un graf neorientat, fiecare nod are un grad de vârf. Deci, este numărul de muchii care sunt incidente în partea de sus. Suma totală a gradelor de noduri este numărul de muchii, înmulțit cu doi: fiecare margine va avea o contribuție, care este egal cu doi.

Vertex cu grad 0 este izolat.

Atarnand nod este un nod cu grad unu.

Teoria grafurilor solicită acest grafic gol în care nu există nici o muchie. Analiza completă - acesta este un grafic obișnuit în care oricare două vârfuri adiacente.

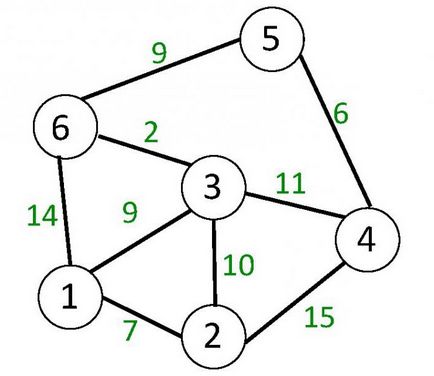
Ponderat grafic - un grafic ale cărui vârfuri sau muchii (arce) din care, sau ambele noduri și muchii (arce) atribuite imediat niște numere. Acestea sunt numite greutăți. A doua figură prezintă un grafic neorientat, ale cărei margini sunt cântărite.

Grafice: izomorfism

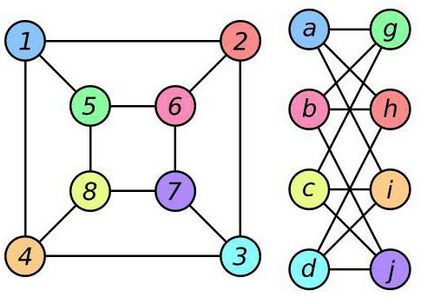
Conceptul izomorfism este utilizat în matematică. În special, teoria grafurilor definește: două grafice U și V sunt izomorfe dacă aceste grafice există bijectie între seturile de noduri: fiecare coloana U 2 noduri conectate printr-o muchie dacă și numai dacă muchia asociată în V grafic același topuri (care poate avea un alt nume). Figura de mai jos prezintă două graficul izomorfe în care nodurile dintre vopsite în aceeași culoare, în prima și în a doua coloană, există o bijectie descrisă mai sus.

Căile și ciclurile

Prin într-un grafic neorientat sau direcționat este o secvență de muchii, în cazul în care fiecare începe succesive în partea de sus, care se termină cel precedent. Un mod simplu - că, în care toate nodurile, cu excepția, probabil, începutul și sfârșitul, iar nervurile sunt diferite. Un ciclu este o cale în digraph, care se potrivesc începutul și sfârșitul vârful și care include cel puțin o nervură. Ciclul într-un grafic neorientat este o cale care conține cel puțin trei muchii diferite. A doua cifră este o buclă, de exemplu, calea (3, 1), (6, 3), (1, 6).

Teoria grafurilor în programarea este folosit pentru a construi un grafic scheme de algoritmi.