Care este puterea
Vă rugăm să rețineți că în această secțiune, înțelege conceptul de grad numai indicator natural și zero.
Conceptul și proprietăți de grade cu indicatori negativi (raționale și fracționare) vor fi luate în considerare în lecțiile la 8 clase.
Deci, vom înțelege că această putere a. Pentru a înregistra numărul de lucrări pe el însuși de mai multe ori se aplică abrevieri.
În schimb funcționează șase multiplicatori identice 4 x 4 x 4 x 4 x 4 x 4 4 6 și să scrie spun "patru până la șase grade."
4 x 4 x 4 x 4 x 4 x 4 = 4 luna iunie
Exprimarea 4 iunie se numește numărul de studii, în cazul în care:
- 4 - baza puterii;
- 6 - exponent.

În general, gradul de bază «a» și indicele «n» este înregistrată de expresia:

Gradul de «o» cu indicele naturale «n», b # 243; 1. lshim este produsul «n» multiplicatori identice, fiecare dintre acestea fiind egal cu numărul de «o».
Înregistrarea «a n» se citește după cum urmează: „într-un grad n» sau «n puterea unui-lea».
Excepția este înregistrarea:
- un 2 - poate fi pronunțată ca „un pătrat“;
- 3 - poate fi pronunțată ca „un cub.“
- 2 - „și cea de a doua măsură„;
- 3 - „și, în al treilea grad.“
Cazuri speciale apar atunci când exponentul este egal cu unul sau zero (n = 1; n = 0).
Puterea de „o“ cu un exponent n = 1 este numărul în sine:
o 1 = a
Orice număr la puterea zero, este egală cu unu.
o 0 = 1
Un zero, în orice fel de grad zero.
0 n = 0
Unitate în orice grad egal cu 1.
1 n = 1
Expresia 0 0 (zero la zero grade) este considerată lipsită de sens.
La decizia din exemplele trebuie amintit că exponentiation se numește găsirea valorilor numerice și alfanumerice după exponentiere.
Exemplu. Crescut la puterea.
- 5 3 = 5 x 5 x 5 = 125
- 2,5 2 = 2,5 x 2,5 = 6,25
- (
gradul de bază (numărul este ridicat) poate fi orice număr - pozitiv, negativ sau zero.
Atunci când numărul exponentiere pozitiv obținut număr pozitiv.
Când ridicarea naturală gradul zero se obține zero.
Când exponentiation număr negativ în rezultatul poate fi un număr pozitiv și un număr negativ. Aceasta depinde de un număr par sau impar a fost exponent.
Luați în considerare exemple exponentiation numere negative.
Din exemplele de mai sus se observă că în cazul în care o valoare negativă este ridicată la un grad impar, obținem un număr negativ. Deoarece produsul dintr-un număr impar de factori negativi în negativ.
În cazul în care un număr negativ este ridicat la nivelul de chotnuyu, se transformă număr pozitiv. Deoarece produsul unui număr par de factori negativi pozitiv.
Un număr negativ ridicat la gradul chotnuyu, există un număr pozitiv.
Un număr negativ ridicat la gradul de ciudat, - numărul este negativ.
Pătratul oricărui număr este un întreg pozitiv sau zero adică:
un 2 ≥ 0 pentru toți o.
- 2 x (-3) 2 = 2 + (-3) + (-3) = 2 * 9 = 18
- · -5 (-2) 3 = -5 · (-8) = 40
Acorde o atenție!
În rezolvarea unor exemple de exponentiation adesea fac greșeli, uitând că înregistrarea (-5) -5 4 și 4 sunt expresii diferite. Datele despre exprimarea rezultatelor exponentiation vor fi diferite.
Calculați (5) 4 este de a găsi valoarea celei de a patra putere a unui număr negativ.
(-5) 4 = (-5) · (5) · (5) · (5) = 625
În timp ce găsiți „-5 4“ înseamnă că proba trebuie să fie rezolvată în 2 etape:
- Ridicat la gradul al patrulea număr pozitiv 5.
05 aprilie = 5 × 5 × 5 × 5 = 625 - Pune în față cu rezultatul „minus“ semn (care este, efectuați o scădere de acțiune).
-5 4 = -625
Exemplu. Calculați: 2 -6 - (-1) 4
2 -6 - (-1) 4 = -37
- 6 2 = 6 · 6 = 36
- -6 2 = -36
- (-1) 4 = (-1) + (-1) + (-1) + (-1) = 1
- - (- 1) 4 = -1
- -36--37 1 =
Procedură Exemple de grade
Calcularea valorilor numite exponentiere de acțiune. Această acțiune este de-a treia etapă.
În expresiile cu grade care nu conțin paranteze, funcționează mai întâi vovzvedenie de putere. apoi înmulțirea și împărțirea. iar la sfârșitul adăugării și scăderea.
În cazul în care expresia are paranteze, primul în ordinea enumerate mai sus efectua acțiuni în paranteze, iar apoi pașii rămași în aceeași ordine de la stânga la dreapta.
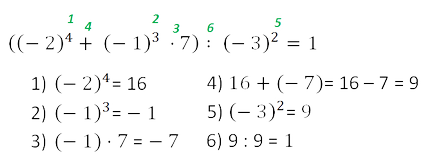
Pentru a facilita rezolvarea exemple utile de a cunoaște și de a folosi puterile din tabel. pe care îl puteți descărca gratuit de pe site-ul nostru.
Pentru a verifica rezultatele, puteți utiliza un calculator de pe site-ul nostru „exponentiation on-line.“