Cea mai mare și cea mai mică valoare a funcției pe intervalul

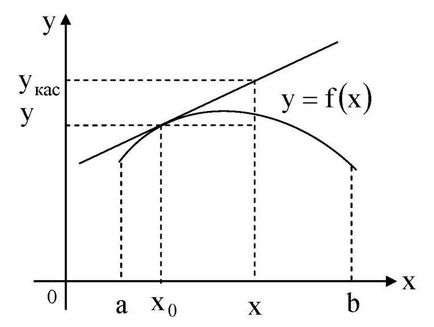
Să presupunem că funcția y = f (x) este continua pe intervalul [a, b]. După cum se știe, o funcție pentru acest interval atinge valorile maxime și minime. Aceste valori de caracteristici pot lua fie punctul intern al intervalului [a, b], sau la limita segmentului.

Pentru găsirea valorilor maxime și minime ale funcției la intervalul [a, b] este necesar:

1) găsi intervalul critic punctul function (a, b);

2) se calculează valorile funcției găsite în punctele critice;

3) calculează valorile funcției la punctele finale, adică la x = a și x = b;

4) a tuturor valorilor calculate ale funcției pentru a selecta cea mai mare și cea mai mică.

Exemplu. Găsiți valorile maxime și minime ale funcției

Găsim punctele critice:

Aceste puncte se află în intervalul [0; 3]; y (1) = - 3; y (2) = - 4; y (0) = - 8; y (3) = 1;

la punctul x = 3 și x = 0.

caracteristici de cercetare privind convexitate și inflexiune punct.

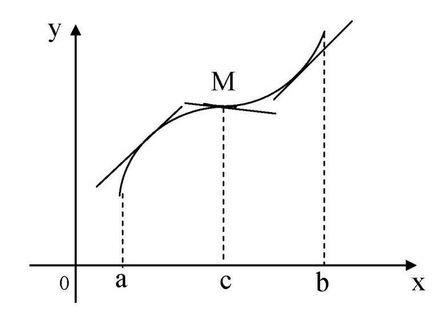
Funcția y = f (x) se numește vypukloyvverh intervalul (a, b). dacă graficul acesteia se află sub tangentă în orice punct al intervalului, și se numește convexă în jos (concav). în cazul în care graficul său se află deasupra tangenta.

Punctul în tranziția prin care o protuberanta se înlocuiește concavitate, sau invers, se numește punct de inflexiune.

Algoritmul de cercetare privind convexitate și inflexiune punct:

1. Punctele critice ale Naydemi doilea tip, adică punctul în care derivata a doua este egal cu zero sau nu există.

2. Aplicați un punct critic pe linia numărul, împărțind-o în intervale. Găsiți semnul derivatei a doua la fiecare interval; dacă funcția este concavă, dacă funcția este convexă în jos.

3. În cazul în care trece prin punctul critic al doilea tip se va schimba semnul și în acest moment al doilea derivat este egala cu zero, acest punct - abscisa punctului de inflexiune. Găsiți ordonata sa.

Asimptotă funcțiilor graficului. Un studiu privind funcția asimptota.

Definiția. Asimptotă a graficului unei funcții este o linie dreaptă. cu proprietatea că distanța de la orice punct din programul de la această linie tinde la zero, cu punctul de îndepărtare a graficului de origine.

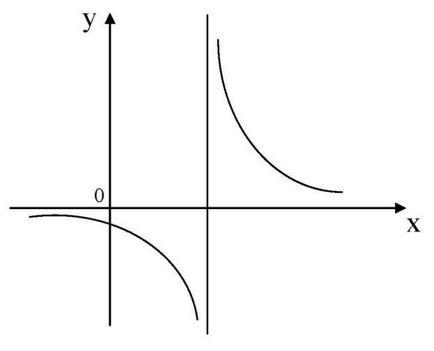
Există trei tipuri de asimptote: verticale, orizontale și oblice.

Definiția. asimptotă Direct nazyvaetsyavertikalnoy graficului y = f (x). în cazul în care cel puțin una dintre funcțiile limite laterale în acest punct este egal cu infinit, adică,

în cazul în care - punctul de discontinuitate, apoi estne aparține domeniului.

x = 2 - punct de pauză.

Definiția. Direct y = Un grafic se numește asimptota orizontală a funcției y = f (x), în cazul în care