mișcare circulară, viteza unghiulară, frecventa, perioada, accelerare centripete

Deoarece viteza liniară schimbă uniform direcție, mișcarea nu poate fi considerată uniformă de-a lungul circumferinței. este uniform accelerată.

viteza unghiulară

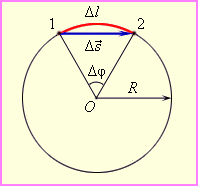
Am alege un punct de pe raza cercului 1. constructului. Pe unitatea de timp punct se mută la punctul 2. La acest unghi raza descrie. viteza unghiulară este numeric egală cu intervalul unghiului de rotire pe unitatea de timp.

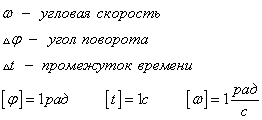
Frecvența și perioada

Perioada de rotație T - este momentul în care organismul face o revoluție.

RPM - numărul de rotații pe secundă.

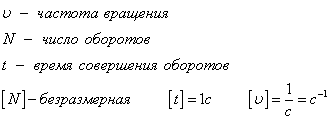
Frecvența și perioada interconectate relație

Comunicarea cu viteza unghiulară

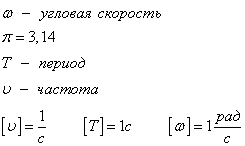
viteza liniară

Fiecare punct de pe cercul se deplasează la o anumită viteză. Această viteză se numește liniară. direcția vectorului viteză lineară coincide întotdeauna cu tangenta la cercul. De exemplu, scântei de mișcare masina de rectificat, viteza instantanee de direcție se repetă.

Luați în considerare un punct de pe cerc, ceea ce face o revoluție, în momentul în care a luat - este o perioadă de T. Way. care depășește punctul - este lungimea circumferinței.

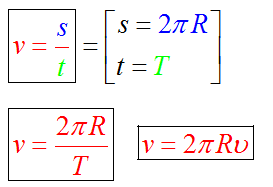
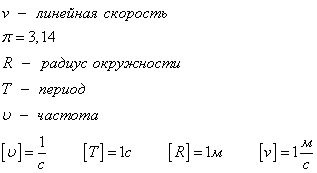
accelerație centripetă

Atunci când se deplasează într-un cerc, vectorul accelerație este întotdeauna perpendicular pe vectorul viteză este îndreptat spre centrul cercului.

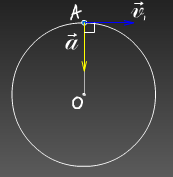
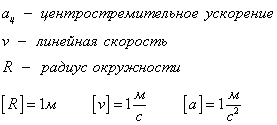
Folosind formulele de mai sus, următoarele relații pot fi derivate

Punctele situate pe o linie dreaptă care emană de la centrul cercului (de exemplu, poate fi puncte care se află pe spițelor), va avea aceeași viteză unghiulară, perioada și frecvența. Asta este, ei se vor roti la fel, dar cu diferite viteze liniare. Mai departe de punctul central, cu atât mai repede se va muta.

Legea din plus de viteză este de asemenea valabilă pentru o mișcare de rotație. Dacă mișcarea corpului sau cadrul de referință nu este uniformă, atunci legea este aplicată vitezelor instantanee. De exemplu, viteza de mers uman pe marginea carusel rotativ, este suma vectorială a vitezei liniare și viteza de rotație a marginii carusel mișcării umane.

Pământul este implicat în două mișcări revoluționare majore: de zi cu zi (pe axa sa) și orbital (în jurul Soarelui). Rotație a Pământului în jurul perioadei de soare de 1 an sau 365 de zile. Pământul în jurul axei sale se rotește de la vest la est, perioada de rotație de la 1 zi sau 24 de ore. Latitude este unghiul dintre planul ecuatorial și direcția centrului Pământului până la un punct a suprafeței sale.

Conform legii a doua a lui Newton este cauza tuturor forței de accelerație. În cazul în care corpul în mișcare trece printr-o accelerare centripete, natura forțelor care sunt cauzate de acțiunea acestei accelerare poate fi diferită. De exemplu, în cazul în care se deplasează de-a lungul corpului unui cerc pe o frânghie atașat la acesta, forța de operare este forța de elasticitate.

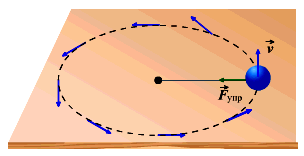
În cazul în care corpul culcat pe discul se rotește cu discul în jurul axei sale, o astfel de forță este forța de frecare. Dacă puterea dispare, corpul va continua să se miște într-o linie dreaptă

Să considerăm mișcarea de la A la punctul B. Viteza circumferențială lineară este vA și vB, respectiv. Rata de schimbare pe unitatea de timp - de accelerare. Noi găsim vectorii diferență.

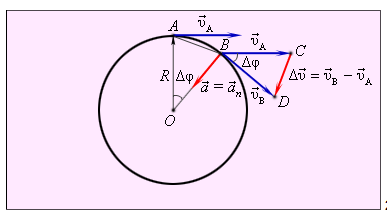
Vectorii de diferență sunt. Din moment ce, obținem

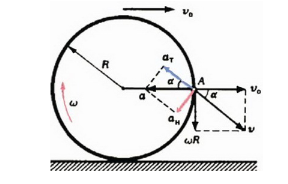
În sistemul de referință asociat cu roata, punctul se rotește uniform pe circumferința razei R la o viteză care variază doar într-o direcție. accelerația centripetă a punctului este îndreptat radial spre centrul cercului.

Acum, să trecem la cadrul fix conectat la sol. accelerație maximă de la punctul A va rămâne valoare și aceeași direcție și absolută precum și în trecerea de la un sistem de referință inerțial la o altă accelerare nu se schimba. Din punctul de vedere al unei traiectorii observator staționar punctele A - nu mai este un cerc, ci o curbă mai complicată (cicloida) de-a lungul căreia se mișcă punctul inegal.

Viteza este determinată de Instantanee formula