Pendulum, și exemple de formula

Pendulum - este punctul de material. suspendat pe un filament inextensibil lung fără greutate (figura 1).

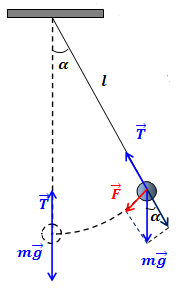
Fig.1. pendulă

Pendulum - un sistem de model pendulează. oscilația liberă a pendulului matematic la unghiuri mici de deviere sunt descrise de oscilații armonice.

În starea de echilibru forța gravitației și forța echilibrului filament elasticitate reciproc, iar punctul de material este în repaus. În cazul unui punct material din poziția de echilibru la un unghi mic la corp va acționa forța care este componenta tangențială a forței de gravitație restaurare:

Această forță este raportată punctul de accelerație tangențial materialul direcționat de-a lungul tangenta la traiectoria. și un punct de material începe să se miște în poziția de echilibru cu creșterea vitezei. După cum se apropie de poziția de echilibru forța de revenire, și, prin urmare, scăderea punctului de accelerație tangențială. La momentul trecerii, unghiul tangențial poziție de accelerare de echilibru a săgeții este de asemenea zero, iar viteza punctului material de maxim. Mai departe punct material trece în poziția de echilibru prin inerție și, se deplasează în direcția opusă forței reduce viteza. Într-o situație extremă punctul de material se oprește și apoi începe să se miște în direcția opusă.

Perioada de oscilație a pendulului matematic

Perioada de oscilație a pendulului matematic este independentă de masa de sarcină și amplitudinea de oscilație.

Exemple de rezolvare a problemelor

Pendulul 1 m lungime variază cu o amplitudine de 1 cm. De ceva timp va fi calea de 1 cm, în cazul în care, la momentul inițial pendulului trece poziția de echilibru? Cât timp va trece pendul: a) prima jumătate a acestui traseu; b) A doua jumătate a acestui fel?

Perioada de oscilație a pendulului matematic este dat de formula:

pendul matematică oscilează. astfel încât deplasarea unui punct material depinde de timp armonic:

Deoarece inițial pendulul trece poziția de echilibru, faza inițială de oscilație este zero.

Calea de 1 cm, adică în acest caz, egală cu amplitudinea oscilațiilor, pendulul va avea loc într-o perioadă de trimestru, adică, timp de 0,5 secunde.

a) În acest caz, compensat:

astfel încât să putem scrie:

b) În cazul în care să treacă tot drumul, de amplitudine egală, pendulul își petrece 0,5 secunde, iar trecerea primei reprize - până la 0,17, în a doua jumătate a modului în care pendulul va cheltui:

Perioada de oscilație a pendulului 2; pe calea de trecere, de amplitudine egală, pendulul va cheltui 0,5; a) pentru prima jumătate a acestui traseu va luat 0,17 secunde; b) în a doua jumătate a modului - de la 0,33.