Structura Cyclic - studopediya

(. Figura 1.3) O trăsătură distinctivă a acestei structuri este prezența în compoziția sa:

- parte în mod repetat cu repetate în timpul calculelor și numit corpul buclei; corpul este liniar tipic sau ramificare structură;

- condiția L, destinate ieșirea timpurie din ciclul.

structuri ciclice vin în două variante: cu condiția prealabilă, adică, verificarea condițiilor de ieșire din buclă înainte de a executa corpul său (a) și un postconditie, implicând condiția de mai sus, după efectuarea corpul buclei (b).

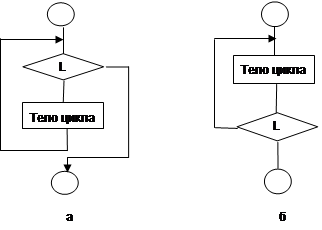
Figura 1.3. Soiurile de structuri ciclice:

a) condiție prealabilă; b) cu postconditia

structurile ciclice sunt utilizate ca elemente separate în dezvoltarea unor algoritmi de calcul a proceselor ciclice (cicluri). Se disting:

1) cicluri cu un număr cunoscut de repetiții ale corpului sau numărul de repetiții, care pot fi evaluate. Aceste cicluri se numesc aritmetică (numărare).

2) numărul de repetiții ale ciclurilor de care nu se cunoaște dinainte și nu se poate calcula - cicluri iterative.

Noțiuni de bază pentru organizarea ciclului, trebuie:

- determina care variabila va gestiona, sau, cum se spune, să servească egoparametrom;

- să formuleze legea de variație a parametrului, și anume specifica modul în care valoarea sa se va schimba după fiecare repetare a corpului;

- determină valoarea numerică la care trebuie furnizate ieșirea din proces ciclic.

Luați în considerare exemplele de procese de calcul algoritmice ciclice menționate în revendicarea 1.

Fie funcția y = sin (x2). Este necesar să se calculeze valoarea în intervalul [a, b], în cazul în care argumentul x se schimba pe acest segment destul de mult specific, predefinit, în mod legal. Deoarece legea de variație a argumentului vom alege cele mai simple, dar în același timp și sunt adesea utilizate de lege

în cazul în care Dx este magnitudinea, numită etapa a argumentului. Substituind valorile formulei i anterior, obținem:

și anume fiecare valoare succesivă a argumentului x este calculat prin însumarea valorii anterioare se incrementează Dx (Figura 1.4). Problema formulată în așa fel este numită problema funcției tabulare.

Ne întoarcem acum la dezvoltarea algoritmului. În această problemă, variabila de control (parametrul ciclului) este un argument funcție, din cauza valorii sale actuale depinde de soluția întrebării dacă să continue executarea în continuare a buclei sau sisteme de calcul și de a ieși din ea.

Dacă următoarea valoare argument este în intervalul [a, b], ciclul se repetă, în timp ce se calculează valoarea corespunzătoare a funcției, altfel ieși din bucla.

Deoarece variația parametrului prezentat în declarația problemei, rămâne să se determine valoarea la care procesul ciclic ar trebui să fie completă. Este evident că această valoare este determinată de inegalitatea xi> b.

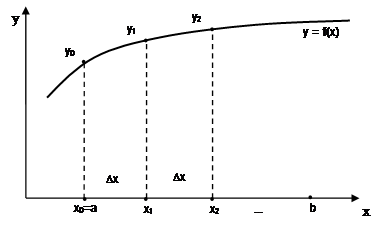
Fig. 1.4. Semnificația geometrică a funcției de sarcini intabulare

Notă. Dacă valoarea inițială a argumentului este etapa b și schimbarea sa este negativ, atunci starea de ieșire în buclă este inegalitatea xi

Vom crea un algoritm sarcinii noastre, bazată pe următoarele:

- valoarea inițială a funcției calculabil argument este cunoscut din condiția problemei x 0 = a, prin urmare, este posibil imediat să se calculeze valoarea corespunzătoare a funcției y 0.

- un alt pas - tabel linie de ieșire care conține valorile argumentului și funcția;

- se calculează în continuare următoarea valoare a argumentului, folosind legea schimbării asupra axei reale xi + 1 = xi + Dx;

- valoare argument xi obținut compara cu valoarea sa de capăt b; În cazul în care se dovedește că xi> b, apoi termina de problema, iar dacă nu - proceda la calcularea următoarea funcție de valoare.

Noi reprezentăm un algoritm ca circuite detaliate și compact.

diagramă detaliată