Unghiuri, matematica

Două linii drepte BA și BC (fig. 13), se intersectează în același punct B, punctul B este format dintr-un colț.

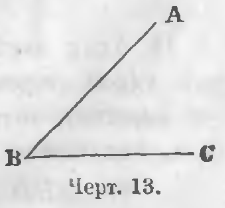
Determinarea unghiului. Unghiul este numit partea nedefinită a planului delimitată de două linii drepte care se intersectează. Unghiul este o cantitate care determină înclinarea unei linii drepte la alta.

Părțile ugla.Peresekayuschiesya linii sunt numite laturi ale unghiului.

Vertex unghiului. Punctul de intersecție a două linii se numește vârful unghiului. Mărimea unghiului este independentă de lungimea laturilor, astfel încât unghiul lateral poate continua la nesfârșit.

Numele unghiului. a) Unghiuri numit scrisoarea, care stă la vârf; astfel încât unghiul din Fig. 13 numit unghiul B. b) În cazul în care în partea superioară a mai multor unghiuri, unghiurile menționate trei litere care stau la partea de sus și cele două părți. În acest caz, scrisoarea din partea de sus a pronunțate și scrise în mijloc.

In Fig. 13, unghiul B numit unghi ABC. BA și BC linia - cele două părți, iar punctul B - vârf al unghiului.

Astfel unghiul ABC este unghiul B sau

ABC = unghiul de colț B.

Unghiul de stele ugla.Slovo znakom∠ înlocuit uneori.

Astfel, ecuația precedentă descrie scris:

În cazul în care punctul de a ieși câteva linii la un punct B, există mai multe unghiuri.

In Fig. 14 din punctul B merge linii drepte BA, BC, BD și în partea de sus a B, există unghiuri ABC, CBD, ABD.

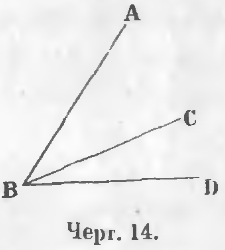
colțuri adiacente. Două unghiuri se numesc adiacente, în cazul în care au de top obscheyu, o parte comună, iar celelalte două sunt pe fiecare parte a părții comune.

unghiurile ABC și CBD (Fig. 14) sunt unghiuri adiacente. Ei au un vârf comun B, laturile generale BC, celelalte două părți BA și BD minciuna una pe partea de sus și cea de mai jos comună BC lateral.

Unghiuri modifica dimensiunea lor, în cazul în care înclinarea este schimbat-o parte în alta. Din două unghiuri având un vârf comun, unghiul care se potrivește în interiorul celălalt colț, este numit un unghi mare. Cifra 14

an. ABD> HS. ABC și HS. CBD <уг. ABD.

Pentru a avea un concept de societate mutuală două unghiuri mai mari având diferite vârfuri, suprapuse un unghi la altul. La aplicarea acestora de a combina partea de sus și în jos o parte, în timp ce cealaltă direcție va permite să compare valoarea lor. Pentru a compara cele două unghiuri ABC și DEF (Fig. 15) este aplicat la unghiul unghiului ABC DEF, astfel încât partea din BC partea EF, punctul E aliniată cu punctul B; apoi ED laterală poate lua trei poziții, poate coincide cu o parte a BA, se încadrează în și în afara unghiului ABC.

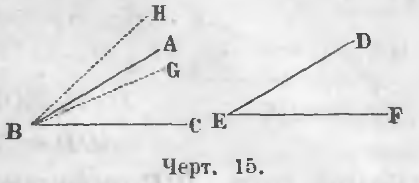
a) Dacă linia ED coincide cu liniile BA, unghiurile sunt numite egale

b) În cazul în care linia ED intră în unghiul ABC și ia poziția BG, unghiul ABC DEF este mai mare unghi

an. ABC> HS. DEF.

c) Dacă linia ED cade ABC colțul exterior de direcție BH, unghiul ABC DEF mai mică decât unghiul

an. ABC <уг. DEF.

Adunare, scădere, înmulțire și împărțire a unghiurilor. Două ABC adiacente și unghiul CBD (Iun. 14) formează un colț ABC. Unghiul ABD se numește suma unghiurilor ABC și CBD. Acest lucru este exprimat în scris de ecuația:

∠ABD = ∠ABC + ∠CBD (a)

De la (a), avem egalitatea:

t. e. ABC este o diferență unghi de unghiuri și CBD DLA, iar unghiul CBD este diferența dintre unghiurile ABD și ABC.

Unghiurile se pot adăuga și scădere.

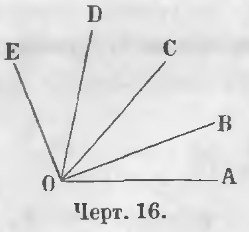
Dacă punctul O (fig. 16) este egală cu mai multe colțuri adiacente, t. E. Dacă

∠AOB = ∠BOC = ∠COD = ∠DOE,

AOC unghi, egală cu suma unghiurilor AOB și BOC este două colțuri AOB,

∠AOC = ∠AOB + ∠BOC, traseu. ∠AOC = 2AOB.

Unghi OCD este de trei colțuri AOB

Pe de altă parte, AOB jumătate unghi este AOC unghi, unghiul de OCD unghi al treilea trimestru AOE.

AOB = ½ AOC = 1/3 = OCD ¼ AOE.

De aici putem trage concluzia că unghiurile cantităților nu numai se pot adăuga și scădere, dar, de asemenea, înmulțirea și împărțirea de către un număr abstract.

Dacă două unghiuri adiacente ACD și DCB (17 iunie), cele două părți CA și CB sunt pe o linie, acestea sunt numite adiacente.

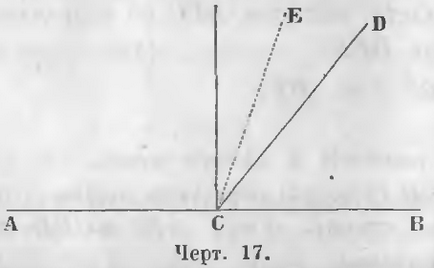
unghiuri adiacente. Unghiurile adiacente sunt cele în care o parte din comun, iar celelalte două sunt pe aceeași linie.

Dacă CD-ul de linie, de cotitură în jurul punctului de C, ia poziția CE, descrescânde recursul unghiului ACD la unghiul ACE, iar recursul unghiul BCD crescând la Î.Hr. unghiului. linie de CD-uri, continuând să se întoarcă, poate accepta o situație în care două de colț adiacente vor fi egale. Când două unghi adiacente ACD și DCB sunt (Iun. 18), acestea sunt numite unghiuri drepte.

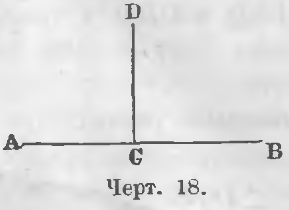
În acest caz, linia de CD-ul se numește perpendicular pe linia AB sau doar perpendicular pe linia AB.

În desen, 19 redactat de un unghi drept, fără alt adiacent acesteia.

Unghi drept este egal cu unul din colțurile adiacente.

În mod normal este o linie dreaptă care se formeaza pe unghi drept altă linie.

În desen, unghiurile 18 și ACD DCB, restul de unghiuri adiacente și egale titlu obținut. Linia DC va fi perpendicular pe linia AB. Această relație reciprocă dintre cele două linii este, uneori, exprimat în scris: CD ⊥ AB.

Deoarece linia AB va fi, de asemenea, perpendicular pe linia CD, linia AB și CD sunt reciproc perpendiculare, t. E. Dacă CD ⊥ AB, apoi AB ⊥ CD.

Talpa perpendicular. punctul de întâlnire reciprocă a două linii perpendiculare numite Soles perpendiculare.

Punctul C (Iun. 18) este perpendicular pe talpa CD.

La fiecare punct al liniei AB poate fi făcută perpendicular pe linia AB.

O perpendicular pe linia (AB), dintr-un punct de pe linie, apoi ridica perpendiculara. Efectuarea perpendiculara (DC) la linia (AB) din punctul (D), situată în afara liniei, apoi să renunțe la o perpendiculară (Fig. 18).

Sloping line. Fiecare linie este non-perpendicular pe o altă linie numită aplecat spre ea.

În figură, linia CE 20 va înclina spre linia AB și CD-ul liniei este perpendicular pe linia AB.

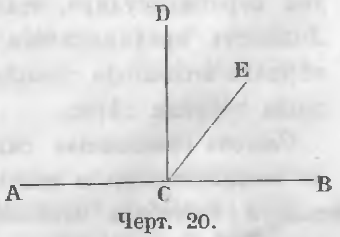
Unghiul BCE mai puțin directă, dar mai mare decât un unghi drept ACE. BCE numit unghi ascuțit și un unghi obtuz ACE.

Acută ugolest orice unghi mai mic de un unghi drept. și ugolest unghi obtuz mai direct.

Același nume, și spre deosebire de colțuri. Două unghi ascuțit sau obtuz numit două omonime și două colțuri dintre care una acuta si una obtuz numite oppositely.

Se formează o linie înclinată CE (fig. 20), cu două unghi adiacente drepte AB, care este mai mică decât una, și alta mai drepte, t. E. O acută și una obtuz.

Teorema 3. Din punct de luat într-o linie dreaptă, puteți ridica la ea, doar un singur perpendicular.

Dată fiind linia AB și un punct de pe ea C (fig. 20).

Trebuie să dovedim. că este posibil să se ridice doar un singur perpendicular.

Dovada. Să presupunem că este posibil din punctul C la linia AB ridica două perpendiculare (. 20 Fig) CD și CE. Prin proprietatea perpendiculara

an. DCB = yi. ACD (a)
an. Ien = yi. ACE.

Dacă aplicăm prima parte a unghiului CED ultima inegalitate, obținem inegalitatea

an. BCE + HS. CED> HS. ACE sau HS. BCD> HS. ACE.

Înlocuirea yi inegalității. BCD ACD egal cu unghiul (a), obținem

an. DCA> HS. ACE,

inegalitate este în mod evident absurd, pentru că o parte nu poate fi mai mult decât întregul ei, prin urmare, presupunând că vă puteți ridica două perpendiculare, duce la absurd, prin urmare, este falsă. Falsitatea ipoteza se bazează pe considerentul că din poziția corectă nu poate fi derivată concluzia greșită, prin urmare, teorema noastră este adevărată.

Metoda pentru a dovedi validitatea acestei teoreme și indicând imposibilitatea absurditatea oricăror alte ipoteze menționate mod dovada de contradicție sau o metodă de a aduce la o absurditate.

Teorema 4. Toate unghiurile drepte sunt egale.

Să presupunem că avem două perechi de unghiuri: (. 21 caracteristici) o pereche de colțuri formează ACD și DCB, și alte colțuri ale EGH HGF și, prin urmare, CD ⊥ AB și HG ⊥ EF.

Trebuie să dovedim că unghiurile sunt egale.

Dovada. Impună linie EF la linia AB punctul G de la punctul C, linia GH du-te apoi pe linia CD, deoarece C poate ridica de la un singur punct de perpendicular, prin urmare, un unghi drept de colț DCB = HGF directă.

Concluzie. Unghi drept este constantă.

Unghiurile de măsură. La măsurarea unghiurilor unui unghi drept ca o valoare constantă, să ia comparația unității. magnitudinea sa este desemnată prin lit. d.

Într-un astfel de caz
orice unghi ascuțit fiecare unghi obtuz> d.

Toate unghiurile sunt exprimate cu o linie dreaptă. De exemplu, să presupunem că unghiul este ½ d, 2/3 d, etc ...

Teorema 5. Suma a două unghiuri adiacente egale cu două dreapta.

Sunt unghiuri adiacente ACD și DCB (fig. 22).

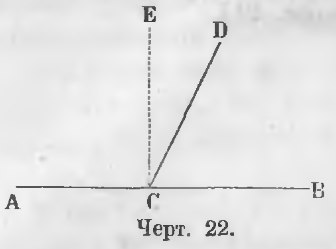
Trebuie să dovedim că ACD + DCB = 2d.

Dovada. Din punctul C erect CE perpendicular, atunci

ACD = ACE + DCE = d + DCE
DCB = BCE - CED = d - DCE

Adăugarea acestor egalitati, avem:

ACD + DCB = ACE + ECB = 2d (QED).

Două alăturate unghi se umfla la două linii și unghiuri sunt, prin urmare, numite complementare.

Teorema 5 urmează investigației. O pereche de unghiuri adiacente este egală cu cealaltă pereche de unghiuri adiacente.

Teorema 6 (revers Teorema 5). Dacă suma celor două unghiuri adiacente egală cu două unghiuri drepte, atunci celelalte două părți sunt coliniare.

Lăsați suma a două unghiuri adiacente ACD și DCB este egală cu două unghiuri drepte (Fig. 23).

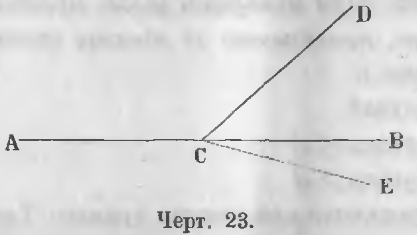
Trebuie să dovedim că linia dreaptă ACB.

Dovada. Să presupunem că ACB are o linie întreruptă, și că continuarea liniei de curent alternativ este linia CE, atunci

Cele două valori sunt egale cu una și aceeași treime egal (axiomă 3), prin urmare,

ACD + DCB = ACD + DCE

pe care o lasă în reducerea

În cele din urmă un ridicol (parte egală cu întregul, a se vedea. Max. 1), prin urmare, linia ACB este o linie dreaptă (după cum este necesar).

Teorema 7. suma unghiurilor având un vârf la un moment dat și dispuse pe o parte a liniei drepte este egal cu doi dreapta.

Unghiurile ACD date, DCE, ECF, FCG, GCB, având un vârf comun la punctul C și dispuse pe o parte a liniei AB (Fig. 24).

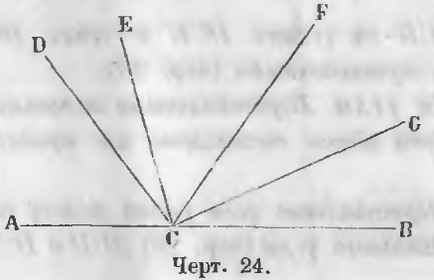
Pentru a dovedi că

ACD + DCE + ECF + FCG + GCB = 2d.

Dovada. Știm că suma a două unghiuri adiacente ACF și FCB egală cu două dreapta (Vol. 5).

Deoarece ACF = ACD + DCE + ECF și FCB = FCG + GCB, înlocuind unghiul ACF FCB și valorile lor, vom găsi:

ACD + DCE + ECF + FCG + GCB = 2d (QED).

Teorema 8. Suma tuturor unghiurilor, aranjate în jurul un punct este egal cu patru drepte.

Având în vedere unghiurile AOB, BOC, COD, DOE, EOA, având un vârf O comună și dispus în jurul punctului O (fig. 25).

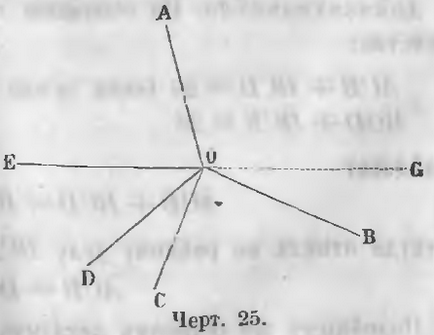
Pentru a dovedi că

AOB + BOC + COD + DOE + EOA = 4d.

Dovada. extinde EO spre OG direcție (Iun. 25), atunci

GOB + BOC + COD + DOE = 2d.

Adăugarea acestor egalitati, avem:

EOA + AOG + GOB + BOC + COD + DOE = 4d.

Deoarece AOG + GOB = AOB,

EOA + AOB + BOC + COD + DOE = 4d (QED).

ACB unghi cu DCE și unghiul unghiul BCD cu verticala un unghi numit ACE (Iun. 26).

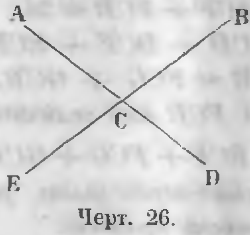
Unghiurile verticale. Unghiurile verticale sunt cele ale căror laturi sunt formate din una dintre părți de a continua un alt unghi.

Teorema 9. Unghiurile verticale sunt egale.

Unghiuri verticale (Iun. 26) și DCE ACB, la fel ca și BCD ACE.

Trebuie să arătăm că ACB = DCE și BCD = ACE.

Dovada. Prin Teorema 5 avem egalitățile:

+ = BCD ACB 2d (suma a două unghiuri adiacente)
BCD + DCE = 2d

ACB + BCD = BCD + DCE

în cazul în care, ținând departe colțul egal al BCD, găsim

În mod similar, arată că

Ravnosekuschaya (bisector) este linia împărțirea în jumătate unghi.

În figura 27 este bisectoarea BD dacă ∠ABD = ∠DBC.

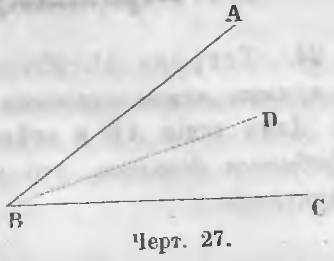
Teorema 10. Bisectoarele două unghiuri adiacente sunt reciproc perpendiculare.

Este unghiuri adiacente și ACB BCD (Iun. 28). Lor linii bisector CE si CF divide unghiuri BCD adiacente și jumătate BCA, deci BCF = FCD, ACE = BCE.

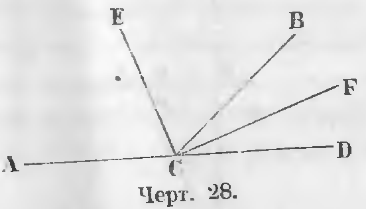
Trebuie să dovedim că CE ⊥ CF.

Dovada. cu condiția

BCE = ½ ACB, BCF = ½ BCD

Adăugarea acestor egalitati, avem:

BCE + BCF = ½ + ½ ACB BCD = ½ (ACB + BCD).

Deoarece ACB + BCD = 2d,

BCE + BCF = ½ · 2d = d.

Întrucât BCE + BCF = ECF,

Unghi ECF linia m. E. CE si CF sunt reciproc perpendiculare linie (QED).