Valorile maxime și minime ale funcției - studopediya
Dacă funcția este continuă pe un interval x închisÎ[A; b]. ea are în mod necesar în acest interval valori maxime (aceasta este una dintre proprietățile funcțiilor continue pe intervalul închis) minim și:
Aceste valori sunt atinse în punctele fie Extrema funcționale în cadrul segmentului sau la punctele finale.
De obicei practica găsirea cele mai mici și cele mai mari valori ale funcției pe segmentul:
1) găsi punctele critice ale intervalului;
2) se calculează valorile funcției găsite în punctele critice;
3) calculează valorile funcției la punctele finale, adică în punctele x = a și x = b;
4) dintre toate valorile calculate ale funcției pentru a selecta cea mai mare și cea mai mică.
Dacă funcția pe intervalul xÎ[A, b], are un singur punct critic și este punctul de maxim (minim), apoi, în acest moment funcția are valoarea cea mai mare (mai mică).
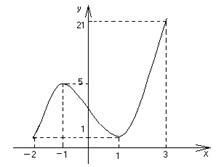
Găsiți cel mai mare și cea mai mică valoare a funcției pe x intervalulÎ[-2, 3].
Din moment. punctele critice ale funcției sunt x1 = -1 și x2 = 1 și ambele aparțin intervalului
[-2; 3]. Comparând valorile funcției la aceste puncte și valorile funcției la capetele de o lungime predeterminată
Am tras concluzia că cea mai mică valoare a funcției este 1, și este atinsă la punctul x = 2 și x = 1 și cea mai mare valoare funcției este egală cu 21 și este atinsă la x = 3.
Toate rezultatele sunt bine ilustrate printr-o diagramă schematică într-un anumit interval.
. xÎ[1, e]. Găsiți și.
La toate punctele acestei funcții predeterminate a segmentului închis este definit și continuu, are un derivat
Ambele punct x1 fix = 0 și x2 nu aparține intervalului [1; e]. Prin urmare, nu există nici un punct critic într-un interval predeterminat (adică, ea își păstrează funcția monotonie). Rămâne să se calculeze valoarea funcției la punctele finale:
grafic al funcției de conducere:
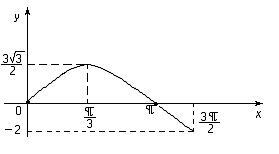
Găsiți cele mai mici și cele mai mari valori ale funcției. .
În această funcție interval închis este continuu și are un derivat.
Ne găsim puncte critice într-o perioadă predeterminată:
Þ Û Û
Se calculează valorile punctelor critice și la capetele intervalului:
grafic al funcției de conducere:
În multe sarcini geometrice, fizice și tehnice necesare pentru a găsi valoarea maximă și minimă de relație funcțională asociată cu o altă valoare. Pentru a rezolva această problemă, trebuie să ne, pe baza condițiilor sale, selectați variabila independentă și exprimă valoarea acestei variabile studiate prin intermediul, și apoi găsi valoarea minimă a funcției de rezultat dorit maxim sau. In acest interval al modificărilor variabile independente pot fi finit sau infinit, este de asemenea determinată de condițiile problemei.
Se determină dimensiunile deschise piscină cu fund pătrat de 32 m 3, astfel încât pereții de linie și fundul ei a mers puțin cantitatea de material.
Cantitatea de material necesar pentru pereții și podeaua piscinei este determinată de suprafața piscină, adică valoarea (m 2). unde
x - este lungimea laturilor unui fund pătrat,
y - este înălțimea de piscină.
După cum este fixat volumul piscinei. valorile lui x și y nu sunt independente, ci sunt legate prin ecuația x 2 y = 32. din care ne găsim.
Apoi, sub rezerva investigarea valorii zonei. exprimată ca o funcție a uneia variabile x independente:
Vom examina această funcție la cea mai mică valoare, reprezentarea grafică a dependenței sale de x:
Þ când x = 4;
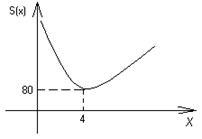
A: piscina dimensiune x m = 4, y = 2 m.
Dintre cele trei scândurile aceeași lățime sudate strâns jgheab pentru alimentarea cu apă. La ce unghi de înclinare a pereților laterali ai jgheabului la partea de jos a ariei secțiunii transversale a jgheabului va fi mai mare?
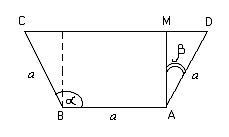
Secțiunea transversală a jgheabului este un trapez isoscel ABCD, în care părțile laterale și baza inferioară egală cu lățimea plăcilor (notate cu a).
Evident, acest domeniu trapezoid depinde de unghiul de înclinare al laturilor bazei inferioare. Dar aici este mult mai convenabil să se introducă ca un unghi variabil independent.
Din zona variabilă a trapez S poate fi scris ca o funcție a unghiului:
. Î . în care, S (0) = a 2. S = 0.
Noi găsim cea mai mare valoare a funcției continue pe intervalul închis:
la Û Û
- singurul punct fix în spațiu.
Să verifice dacă acesta este punctul maxim, folosind derivata a doua:
dacă funcția are un maxim (a doua condiții de optimalitate suficiente).
Deoarece acest maxim este singura extremelor în intervalul, și oferă cea mai mare valoare a funcției.
Găsirea. îndeplinește condițiile problemei, vom calcula.
Găsiți valoarea minimă și maximă a funcției pe un interval închis.