Decizia de intervalele inegalitati

1. Pentru a generaliza utilizarea metodei de intervale pentru a aborda inegalitățile
2. Afișați oportunitățile acestei metode de rezolvare a inegalităților care conțin variabile, sub marca jurnal, și funcții trigonometrice.

Vom lua în considerare inegalitatea, partea dreapta este egală cu zero, iar partea stângă este reprezentat sub forma unui produs sau funcții private.

Ideea metodei: Semnul lucrării sau privat determinate de semnul factorilor.

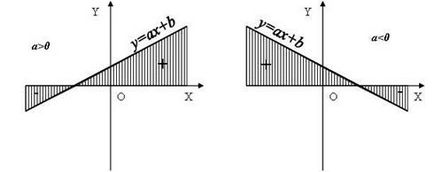
O funcție liniară, cu o pantă nenul schimbă semnul când se trece prin zero a funcției, cu dreptul funcției mărcii de zero coincide cu semnul pantei.

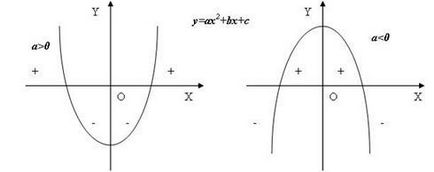
trinom pătrat cu D> 0 când trece prin fiecare zero al funcției schimba semnul, cu o regulă de pătrat semn rădăcină trinomul coincide cu coeficientul său de conducere. [1]

Aceste considerații conduc la următoarele soluții Schema de inegalitate:

1. Găsim zerourile numărătorul: ,,.
2. Găsim zerourile numitorul :.
3. Desenați zerouri punct de pe axa reală. pentru că inegalitate este strictă, atunci toate zerourile descriu puncții care se rup pe axa intervale numerice:

In dreapta sunt semnul fiecărui factor coincide cu coeficientul său de conducere:

Prin urmare, fracțiunea de acest decalaj este de asemenea negativ.

1. Atunci când trece prin fiecare dintre marcate zero, unul și numai un singur factor de modificări semna, și așa mai departe de fiecare dată când am împușcat marca. În acest sens, am loc în intervalele de semne (așa cum se arată în figura 3).
2. Selectați intervalele la care fracția este negativă.
3. Scrieți răspunsul.

În exemplul 1, semnele în intervalele de funcții alternative semn constant. Cu toate acestea, pentru a generaliza că acest lucru se va întâmpla întotdeauna, desigur, nu ar trebui să fie.

-2 - zero, a doua multitudine

am pus zerouri găsit pe axa reală, deoarece inegalitate nu este strictă, atunci zerourile numărătorul reprezentat de puncte umbrite, și dispariția numitorului noi, deoarece puncții acest număr nu este inclus în domeniul inegalității:

Notăm zero, a doua multiplicitate de căpușă, să nu uităm. pentru că numărătorul este întotdeauna ia valori pozitive, atunci intervalul de caractere din dreapta va depinde de semnul coeficientului de conducere al numitorului, adică, "+". În partea stângă a „1“ este numitor negativ și numărătorul pozitiv, prin urmare, atunci când trece prin numerele -2 semn nu se schimbă:

Acest lucru va ajuta să înțeleagă următoarea imagine geometrică (Figura 6):

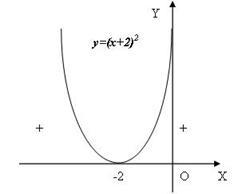
1. Pentru a înregistra răspunsul pentru a alege un decalaj în cazul în care există un semn „+“ și punctul umbrit la care fracțiunea este zero.
   răspundă:

Concluzie: trecerea prin zero chiar și multiplicitate, semnul nu se schimbă.

Pentru a rezolva variantele, urmate de o discuție în bord.

1. zerourile numărătorul:
   - zero, a doua multitudine

zerouri ale numitorul:

;
- a treia zero a multiplicității

Metoda de intervale de aplicare nu se limitează la decizia inegalităților raționale.

Flexibilitatea metodei se bazează pe o proprietate vizuală suficient funcțiilor continue „Dacă intervalul (a, b) funcția f (x) este continuă și nu devine zero, atunci acest interval reține semn.“

Vom rezolva această inegalitate prin aceeași schemă, ci pe întreaga linie, și pe domeniul funcției logaritmică, adică, în intervalul (*):

Prin urmare, în acest interval de partea din stânga este negativă

1. atunci când trece prin fiecare rădăcină schimbă semnul unul și numai unul dintre factorii. Având în vedere acest lucru, vom plasa semnele în golurile rămase.

zerouri ale numitorul:

soluția este reprezentată pe fig. 10:

trinom Square din numărătorul nu are rădăcini și nu se schimbă semnul său. semnul său coincide cu semnul coeficientului de conducere, adică "+".

Dăm la acest tip de inegalitate în partea dreaptă a fost un „0“:

1. zerouri ale numitorul:
   
2. soluția este reprezentată pe fig. 11:

, dar satisface numai DHS

1. soluția este reprezentată pe fig. 13:

Atribuirea acasă (decizia acordată în Anexa1)

Sarcini pentru activități extrașcolare prevăzute în Prilozhenii2.

Concluzie: După cum se știe, liniar, funcții pătratice, exponențială, exponențiale, logaritmice și trigonometrice, precum și compoziția lor și funcțiile derivate din ele prin intermediul unor operații aritmetice sunt continue în domeniul său. Prin urmare, metoda de intervale pot fi folosite în rezolvarea aproape toate curs inegalitățile de școală. intervale metoda prezentă permite o multitudine de soluții ale inegalității ca uniune de intervale ale căror limite sau rădăcinile ecuației sau punctele de delimitare ale definiției.

[1] "Metoda interval" // "Quantum" revista No12, 1985