grafice Euler - studopediya

Celebra problema Euler a podurilor Koenigsberg, limbajul articulat de grafice în 1736 a dat naștere la o teorie matematică grafic. Această problemă joc, esența, care este după cum urmează: în orașul Königsberg pe râul Pregel, există două insule, care sunt conectate între ele și malurile șapte poduri, așa cum se arată în Fig.34. Plimbare în jurul orașului, și din moment ce mișcarea din orice punct, pe care doriți să treacă prin fiecare pod exact o dată și pentru a reveni la punctul de plecare.

Pentru fiecare nod din suprafața de teren, iar fiecare pod - margine. Apoi, „planul de oraș“ va apărea așa cum se arată în figura 35. Și acum problema poate fi reformulate pentru grafice: găsi într-un grafic conectat un circuit închis care trece prin fiecare dintre marginile sale, sau, cum se spune, acoperă toate marginile graficului. Un astfel de lanț este numit Euler-lanț sau ciclu Eulerian. și grafice în care există un astfel de lanț, numit grafice Euler. Evident, graficul prezentat în figura 35, Euler nu este. Graficul din figura 36 - Euler și lanțul corespunzător Euler - o secvență de muchii (1,2, ¼, 12).

Un grafic se numește polueylerovym. în cazul în care există un Euler circuit deschis în acesta, adică, lanț, acoperind toate muchiile graficului, în care vârfurile inițiale și finale nu coincid. Și, în sfârșit, graficul este numit neeylerovym. în cazul în care nu există nici deschis sau un circuit închis Euler. În Figura 37 (stânga) - graficul polueylerov în Figura 37 (dreapta) - graficul neeylerov.

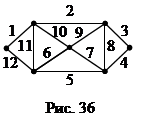
Teorema 3.13.1. Graficul conectat este Eulerian dacă și numai dacă fiecare nod are chiar grad.

Dovada: (a) Să presupunem că graficul este Eulerian și C - ciclul Euler. Apoi, trecând pe marginea cu fiecare dintre nodurile, vom crește cu 2 grade, ci pentru că fiecare margine a graficului este găsit în C exact o dată, gradul de fiecare nod va fi un număr par.

(B) Acum, să fiecare vârf are chiar grad, adică deg (vi) ³2 pentru orice număr nod i. Prin urmare, graficul nu are noduri pandantiv, și nu este un copac. Prin urmare, în coloana trebuie să fie cel puțin un ciclu, chiar dacă C1. Luați în considerare graficul G1 = G \ C1. Fiecare nod al G1 trebuie să aibă chiar grad, deoarece toate nodurile au grad C1 2. Cu toate acestea, este posibil ca G1 - graficul deconectat. Dacă G1 este format din vârfuri izolate, adică, deg (vi) = 0 pentru toți i. ciclul C1 - iar teorema Euler a demonstrat, dacă acest lucru nu este așa, atunci fiecare G1 component - este un grafic conectat cu nodurile chiar grad, iar fiecare component are cel puțin un ciclu. (Putem presupune că G1 este format din vârfuri izolate și o singură componentă conectată). Lăsați acest ciclu C2 1, C2 2, ¼, C2K. Luați în considerare acum graficul G2 = G1 \ C2. unde C2 =. La fel ca înainte de gradul de fiecare nod al graficului G2 - o chiar sau zero. Dacă G2 este format din vârfuri izolate, atunci graful are un ciclu Euler, care poate fi obținut după cum urmează: du-te la ciclul C1 coaste atâta timp cât îndeplinesc sus aparținând oricărei componente a graficului G1 (aceste noduri sunt obligate să aibă, deoarece . graficul original este conectat). Apoi vom trece prin ciclul componentelor, și apoi continuă să se deplaseze de-a lungul marginilor C1. până la următoarele componente vertex se întâlnesc și du-te la ciclul Rib al acestei componente, apoi din nou se deplasează pe următoarele componente C1, etc. Noi mergem în jurul valorii de toate marginile graficului exact o dată și pentru a reveni la vârful de pornire. Dacă G2 are un top neizolata, atunci ele formează componentele conectate, fiecare dintre care are cel puțin un ciclu C3 1, C3 2, ¼, C3k. În continuare, să ia în considerare graficul G3 = G2 \ C3. unde C3 =. Dacă G3 este format din vârfuri izolate, atunci teorema este dovedit și poate fi specificat ciclu Euler procedura. In caz contrar, eliminați toate ciclurile G3 și acționează astfel încât până atunci, până când un grafic care constă numai din vârfuri izolate.

Corolar 1: O familie de nervurilor graficului Euler poate fi împărțit în cicluri disjuncte în coaste.

Corolar 2: Euler fiecare vârf al graficului este conținut în cel puțin un ciclu.

Teorema 3.13.2. În orice grafic conectat cu vârfurile 2k impare ale unei familii de circuite k (care nu se intersectează coaste), care împreună acoperă toate marginile graficului.

Dovada: Notăm nodurile impare: A1. A2. ¼, Ak. B1. B2. ¼, Bk - în toate nodurile 2k. Adăugați la contoriza k nervurilor (A1, B1), (A2, B2), ¼, (Ak, Bk). Acum, toate nodurile au chiar grad, și există un ciclu Eulerian. Eliminarea coaste k scrise, pentru a rupe lanțurile ciclu k conținând toate marginile graficului inițial.

Corolar. Earl este polueylerovym dacă și numai dacă are exact două noduri de grad impar. Evident, unul dintre aceste noduri vor începe pentru a deschide graficul de lanț Euler, iar celălalt - în final.

Luați în considerare algoritmul de construire Fleury Euler lanțului în graficul Eulerian.

Fie G - Euler grafic, atunci următoarea procedură este întotdeauna posibil, și conduce la circuitul grafic Euler G. primește de la un nod arbitrar, du-te de-a lungul marginilor unui mod arbitrar, respectând numai următoarele reguli: 1) pentru a șterge marginile pe măsură ce trec și șterge noduri izolate, de asemenea, care sunt astfel formate; 2) în fiecare etapă a merge peste pod numai atunci când nu există alte posibilități.